栄光学園中学校・高等学校算数過去問研究
栄光学園中学校算数入試問題の特徴は、思考力を問う出題です。
今回は、2018年度算数入試問題から3.円柱形のおもりを水槽に入れる問題を解説します。おもりの体積分だけ水かさが増えることに注意して解きましょう。
算数入試問題 円柱形のおもりを水槽に入れる問題にチャレンジ
栄光学園中学校2018年度 算数入試問題 3.割合問題
栄光学園中学校2018年度 算数入試問題 3.割合 (1) 解説解答
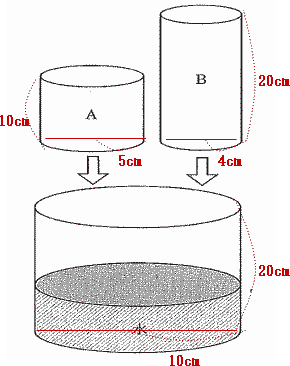
(1) ある高さまで水が入った容器にAとBのおもりを入れたところ、下の図のように容はちょうど満水になりました。容器にはもともと何cmの高さまで水が入っていたか答えなさい。
解説
円柱の容器の容積は 10×10×3.14×20 = 2000×3.14c㎥
よって 容器にもともと入っていた水の体積は
2000×3.14 – 570×3.14 = 1430×3.14c㎥
したがって、おもりを入れる前に入っていた水の高さは
1430×3.14÷(10×10×3.14) = 14.3
答え 14.3cm
栄光学園中学校2018年度 算数入試問題 3.割合 (2) ①解説解答
(2) 6cmの高さまで水の入った容器にAとBのおもりを、まずA,その後でBの順に入れました。① Aのおもりを入れると水位は何cmになるか答えなさい。
解説
面積図の通り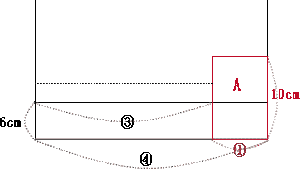
水そうとおもりAの底面積の比は 10×10:5×5 = 4:1
①×6 = (④ – ①)×□
□ = 2cm
よって 水位は 6 + 2 = 8cm
答え 8cm
栄光学園中学校2018年度 算数入試問題 3.割合 (2) ②解説解答
② Bのおもりを入れると水位は何cmになるか答えなさい。
解説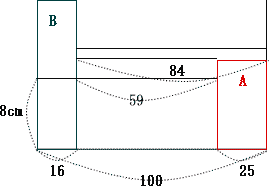
水そうとおもりA、おもりBのそれぞれの底面積の比は10×10:5×5:4×4 = 100:25:16
おもりAを入れたあとの水位は8cm
おもりBを入れることによって押しのけられる水量は 16×8 = 128
おもりA,Bを除いた水そうの底面積は 100 -( 25 + 16) = 59
Aと同じ高さまでに入る水の量は 59×2 = 118
よって 残り128 – 118 = 10はおもりBの底面積以外の底面積の高さの分だけ水位が上がるので、
10 ÷(100 – 16) = 0.11・・・
したがって 水位は 10 + 0.1 = 10.1cm
答 10.1cm
栄光学園中学校2018年度 算数入試問題 3.割合 (3) 解説解答
(3) ある高さまで水が入った容器に、A,Bの順におもりを入れたときとB,Aの順におもりを入れたときとでは、2つのおもりを入れる前と後の水位の差が等しくなりました。容器には問題としてもともと何cmの高さまで水が入っていたか答えなさい。求め方も書きなさい。ただし、水はあふれなかったものとします。
解説
おもりAだけが入っているときと、おもりBだけが入っているときの水位が等しいときを考える。水位が10cm以下のとき、おもりA,Bの底面積に差があるので、水位にも差が生じる。よっておもりA,Bをそれぞれ入れたときの水位が10cmを超える場合となる。
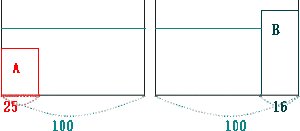
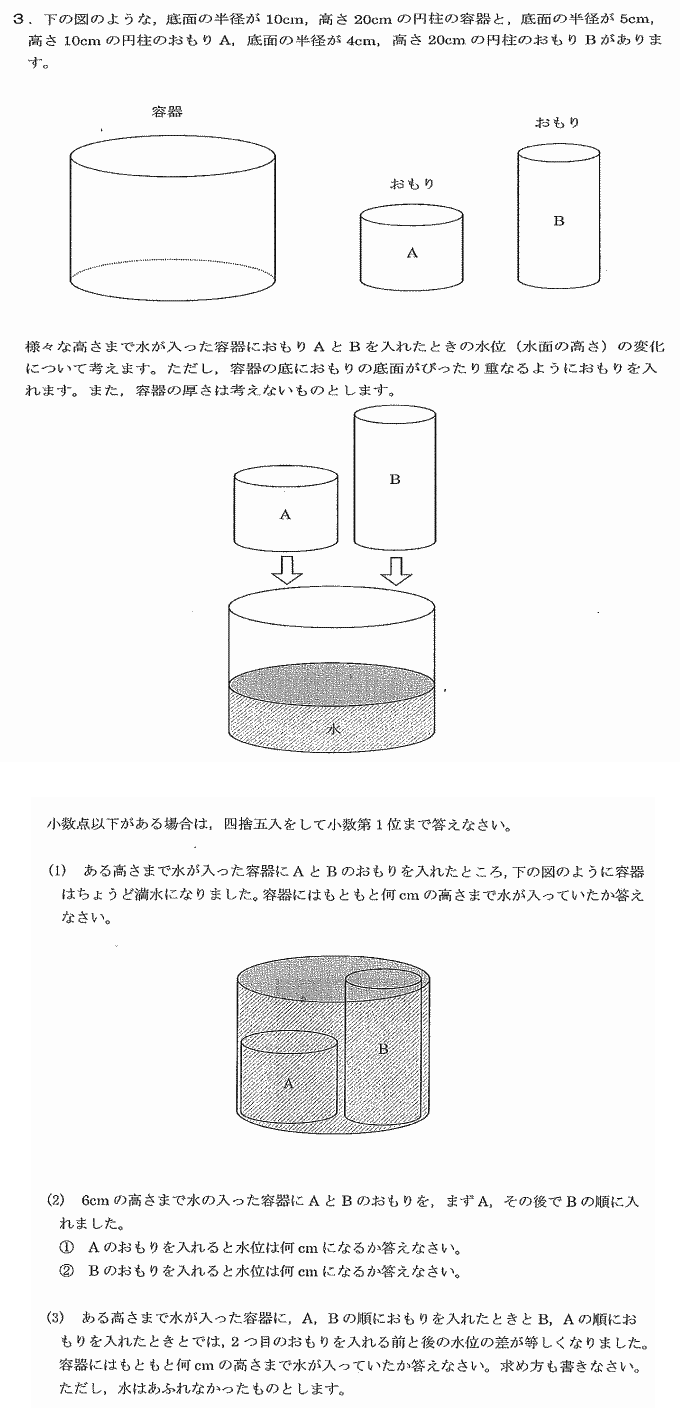
上図の通り、おもりAの体積とおもりBの水位までの体積が等しいときなので、この時の水位は