浅野中学過去問対策

2020年度浅野中学算数入試問題は　1.小問集合5問，2.浅野中学が創立100周年にちなんでの出題。3.ニュートン算　4.空間上をひもが動く問題　5.ほしがたの多角形の角度の和の問題　が出題されました。

今回は1.小問集合(5)の鳩の巣原理を解説します。

鳩の巣原理は、小学校では学習せず高校の数学A整数の性質で学習します。

昨日、担当している麻布中学2年の生徒に鳩の巣原理について知っているかとたずねました。麻布中の一年の時はオリジナル問題冊子で学習し、中二の今はまだ週一の登校日以外はまだオンライン指導が続いていますが、数学のオンライン授業で5月か6月に教わったばかりだとのことでした。鳩の巣理論は中学の教科書で学習する内容ではありません。

中学受験の進学塾では、誘導付きで入試問題で出題されたあと市販の問題集に載せられたり、塾・予備校で取り上げられたりすることがあります。この出題も、知っている人は知っているという種類の問題だと思います。

浅野中学校2020年度　算数入試問題　1.小問集合 (5)　鳩の巣原理　問題

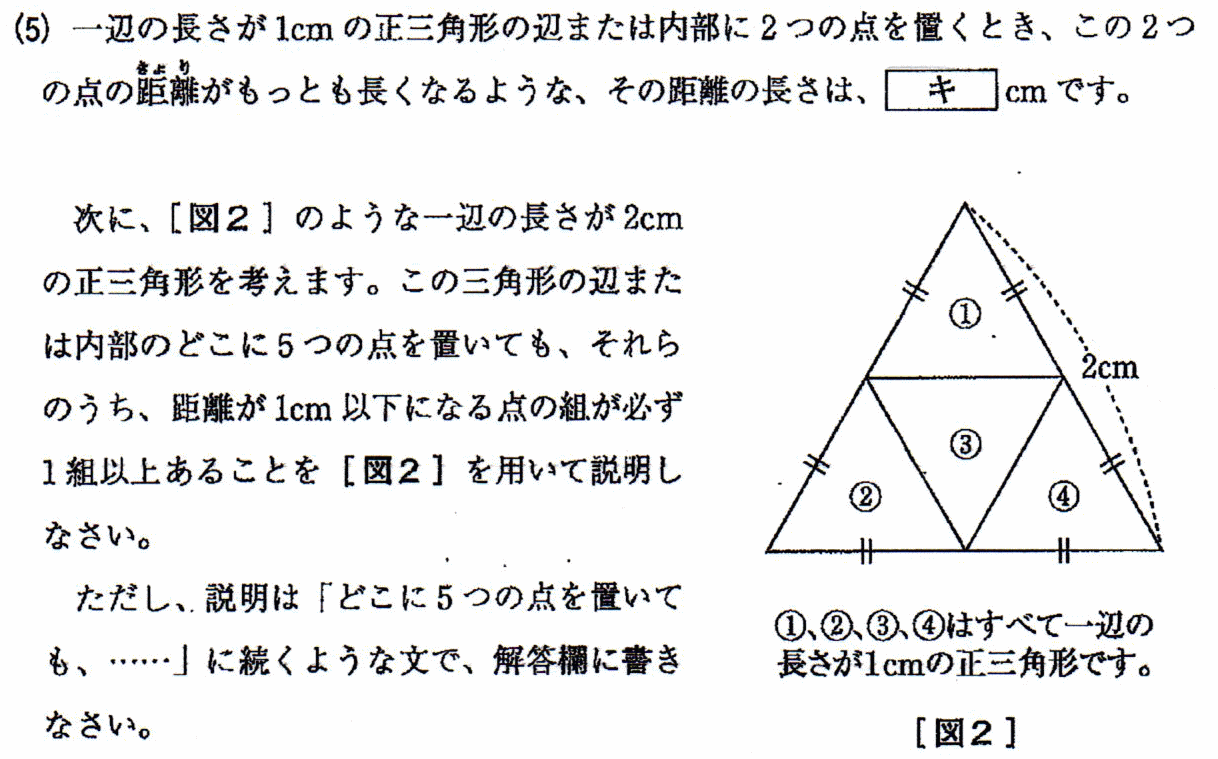
浅野中学校2020年度　算数入試問題　1.小問集合 (5)　鳩の巣原理　解説解答

どこに5つの点を置いても、距離が1cm以下にになる点の組が必ず1組以上ある。

図で一辺1cmの正三角形の辺または内部に2つの点を置くときその最大距離は1cmなので、一つの正三角形の辺および内部に1cmを越えて2つの点をおくことはできない。

1辺2cmの正三角形内部には1辺1cmの正三角形は4個出来るが、1辺1cmの正三角形の辺および内部には1cmをこえた距離の2点をおくことはできない。

4個の点を4個の正三角形に一つずつ置くとき、互いに1cmより大きい距離に点をそれぞれ1点ずつ置くことが出来る。

5個目の点を置くときには、4個の正三角形のどれかの辺や内部に置かなければならない。

そうなれば一つの正三角形の辺および内部に2点あることになる。そのため少なくとも1組の2点の距離は1cm以下になる。

答え　キ　1cm，　　説明　(どこに5つの点をおいても,)　①～④のどれかの辺または内部に2つおかれるから。