東京都市大学等々力中学校S特選過去問対策
東京都市大学等々力中学校では、「都市大等々力改革第1ステージ」として2010年に共学部を新設し、様々な教育プログラムの創出と入試制度改革を行って参りました。共学立ち上げ時は特別選抜コース(特選)・特別進学コース(特進)の2コースで募集を始め、その後2014年に帰国生入試・英語選択入試を導入しました。これは海外での貴重な経験を持った生徒の入学により、一般生徒へ与える良い意味での波及効果を期待するものです。
2015年からは「都市大等々力改革第2ステージ」に入り、従来の特選・特進コースに加え、更に難関国公立大を目指すS特選コースを新設し、3コース体制へと変更しました。
2017年には、2020年以降の大学入試改革を見据え、従来の入試とは異なるAL(アクティブラーニング)入試(思考力・協働力テスト)を導入することにより、今後の大学側が求める「自主的な学びのできる生徒」の発掘にも乗り出しました。
更に2018年では算数1教科入試を新設し、初めて見るものにもひるむことなく、継続して物事に取り組め、思考の組み立てのできる生徒を求めることとしました。2019年度は英語選択入試を英語1教科入試に変更し、都市大等々力の「特色入試」の充実を図ります。
このように都市大等々力の「特色入試(帰国生入試・英語1教科入試・AL(思考力・協働力テスト)入試・算数1教科入試)は多種彩々な才能を持つ生徒を求め、入学後にその才能を活かし、お互いに刺激し合い、切磋琢磨し才能を開花させてもらいたいと考えています。
2023年度都市大学等々力中学校帰国生入学試験は 募集人数男女20名に対し、志願者男子137名 女子55名 受験者男子115名 女子51名 合格者男子81名 女子41名でした。
帰国生算数入試問題は 1.四則計算3問 2.小問集合5問 3.食塩水の濃度 4.平面図形の相似比と面積比 5.旅人算 6.正十二角形上の三角形の数が出題されました。
今回は6.正十二角形上の三角形の数の問題を解説します。
プロ家庭教師集団スペースONEの中学受験合格のための過去問対策へ
東京都市大学等々力中学校2023年度帰国生算数入試問題6.正十二角形上の三角形の数の問題
東京都市大学等々力中学校2023年度帰国生算数入試問題6.正十二角形上の三角形の数の問題(1)解説解答
( 1 )正十二角形の2つの辺を使ってつくることができる三角形は何個ありますか。
解説解答
1つの頂点を決めるときの他の2点の数を考える。
1点がAのとき、B,C,D,E,F,G,H,I,J,K,Lの11点から2点を選ぶ組み合わせ
(B,C)(B,D)(B,E)(B,F)(B,G)(B,H)(B,I)(B,J)(B,K)(B,L)
(C,D)(C,E)(C,F)(C,G)(C,H)(C,I)(C,J)(CK)(C,L)
(D,E)(D,F)(D,G)(D,H)(D,I)(D,J)(D,K)(D,L)(
(E,F)(E,G)(E,H)(E,I)(E,J)(E,K)(E,L)
(F,G)(F,H)(F,I)(F,j)(F,J)(F,K)(F,l)
(G,H)(G,I)(G,J)(G,K)(G,L)
(H,I)(H,J)(H,K)(H,L)
(I,J)(I,K)(I,L)
(J,K)(J,L)
(K,L) 11×10÷2 = 55個
1点がBのとき、A,Bを除くC,D,E,F,G,H,I,J,K,Lの10点から2点を選ぶ組み合わせ
10×9÷2 = 45個
同様に 1点がCのとき、A,B,Cを除くD,E,F,G,H,I,J,K,Lの9点から2点を選ぶ組み合わせ
9×8 ÷2 = 36個
1点がDのとき A,B,C,Dを除く8点から2点を選ぶ組み合わせ
8 ×7÷2 = 28個
1点がEのとき A,B,C,D,Eを除く7点から2点を選ぶ組み合わせ
7×6÷2 = 21個
1点がFのとき A,B,C,D,E,Fを除く6点から2点を選ぶ組み合わせ
6×5÷2 = 15個
1点がGのとき A,B,C,D,E,F,Gを除く5点から2点を選ぶ組み合わせ
5×4÷2 = 10個
1点がHのとき A,B,C,D,E,F,G,Hを除く4点から2点を選ぶ組み合わせ
4×3÷2 = 6通り
1点がIのとき、A,B,C,D,E,F,g,H,Iを除く3点から2点をえらう組み合わせ
3×2÷2 = 3個
1点がJのとき、A,B,C,D,E,F,G,H,I,Jを除く2点の組み合わせ 1個
以上から 55 + 45 +36 + 28 + 21 + 15 + 10 + 6 + 3 + 1 = 220
答え 220個
別解 12点から3点を選ぶ選び方で重複する選び方を除くので![]()
答え 220個
東京都市大学等々力中学校2023年度帰国生算数入試問題6.正十二角形上の三角形の数の問題(2)解説解答
( 2 )正三角形は何個ありますか。
解説解答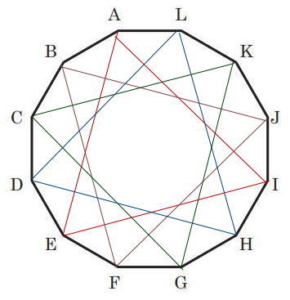
12点のうち等間隔に3点を選ぶ。
12÷3 = 4 よって 4点ごと(間に3点)の頂点を結ぶ。
(A,E,I)(B,F,J)(C,G,K)((D,H,L) 以上4個
答え 4個
東京都市大学等々力中学校2023年度帰国生算数入試問題6.正十二角形上の三角形の数の問題(3)解説解答
( 3 )二等辺三角形(正三角形は除く)は何個ありますか。
解説解答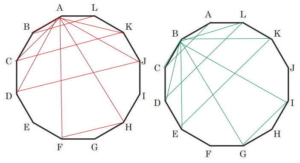
頂角をAとしたときの残りの点の決め方は(B,L),(C,K),(D,J),(F,H)の4つ。
頂角をB,C,D,E,・・・Lとしても同様に4つずつあるから4×12=48個
答え 48個
