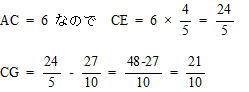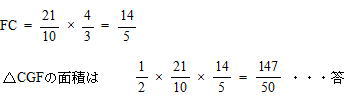MENU

記事の作成者：プロ家庭教師集団スペースONEとは

最新情報

  • HOME
    •  > 
  • 過去問対策
    •  > 
  • 桐光学園高校2023年度数学入試問題5.平面図形

    • 2023/02/15

    • 高
    • オ
    • 過去問対策

    桐光学園高校2023年度数学入試問題5.平面図形

    桐光学園高等学校過去問研究

     

    2023年度桐光高等学校第1回入学試験は2月10日に実施されました。

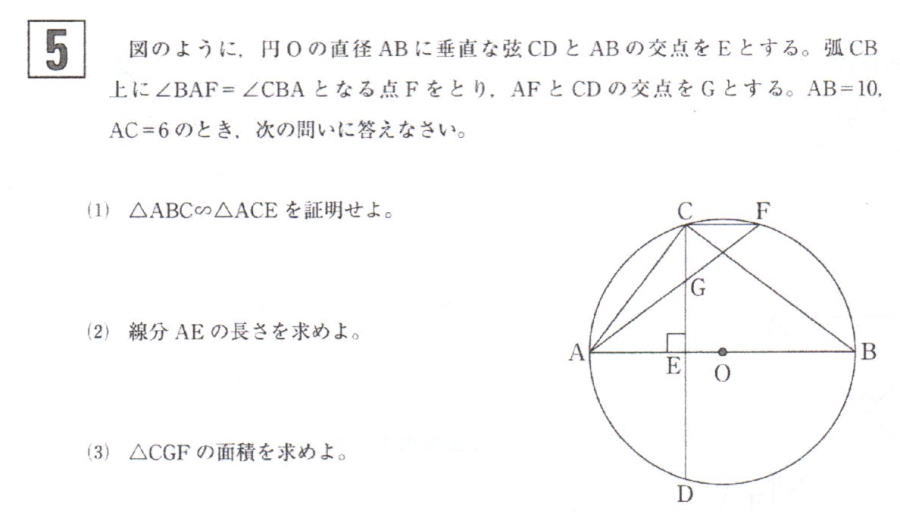
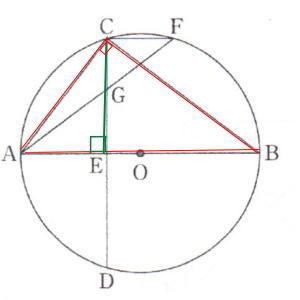
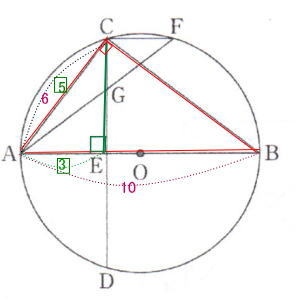
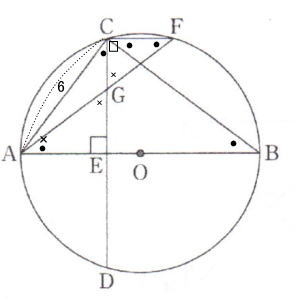
    第1回数学入試問題は　1.四則計算5問，2.小問集合6問,　3．確率，4.関数，5．平面図形(円の性質と相似形)が出題されました。証明以外は途中式を必要としない解答のみを書きます。

    数学は1,2の小問集合は教科書基本～標準問題です。大問も枝問1.2も標準レベルです。取りこぼしをしないように標準レベルの問題を繰り返し学習しましょう。

    今回は5.平面図形を解説します。相似比で辺の長さを丹念にだしていきましょう。

    プロ家庭教師集団スペースONEの高校受験合格のための過去問傾向と対策へ


    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

    桐光学園高校2023年度数学入試問題5.平面図形　問題

    桐光学園高校数字入試問題解説解答

    桐光学園高校2023年度数学入試問題5.平面図形(1)解説解答

    (1)　△ABC ∽ △ACEを証明せよ。

    証明

    桐光学園高校過去問解説

    △ABC と △ACEにおいて

    ∠BCA = 90°(直径ABの円周角)，∠CEA = 90°(仮定)　より　∠BCA = ∠CEA・・・①

    ∠CAB = ∠EAC(共通)・・・②

    ①，②より　二角相等なので　△ABC ∽ △ACE


    桐光学園高校2023年度数学入試問題5.平面図形(2)解説解答

    (2)　線分AEの長さを求めよ。

    解説解答

    円周角の定理

    (1)より　△ABC ∽ △ACE

    AB：CA = AC：EA　AB = 10，CA = 6なので

    高校入試プロ家庭教師

    桐光学園高校2023年度数学入試問題5.平面図形(3)解説解答

    (3)　△CGFの面積を求めよ。

    解説解答

    高校入試問題相似形

    ∠CBA = ∠CFG (弧CAの円周角)，∠BAF = ∠FCG(弧FBの円周角)　錯角が等しいので　CF // AB

    したがって　∠FCG = ∠CEA = 90°

    △ACEと△GAEにおいて

    ∠EAG = ∠ABC(仮定)
    (1)より　∠ACE = ∠ABC　∠ACE = ∠EAG，∠CEA = ∠AEG = 90°

    二角相等なので　△ACE ∽ △GAE

    また　△GAEと△GFCにおいて　

    ∠GAE = ∠GFC，∠AEG = ∠FCG = 90°　二角相等より　△GAE ∽ △GFC

    △ABCの辺の比はAB：BC：CA = 5：4：3

    AE：EG = 4：3

    高校受験数学プロ家庭教師
    AC：CE = 5：4

    高校入試家庭教師

    CG：FC = 3：4

    神奈川私立高校入試問題

    合格者お喜びの声はこちら

    各種お問い合わせにつきましては、下記よりお気楽にお問い合わせください。

    お問い合わせはこちら
    メールでお問い合わせ
    LINEでお問い合わせ

    オンライン家庭教師も在籍中！「お問い合わせ種別」の欄を選択ください。

    営業時間：AM 10:00 〜PM 9:00