和洋国府台女子高校過去問研究

和洋国府台女子高校2022年度数学入試問題11.三角形の角の二等分線の定理の証明　問題

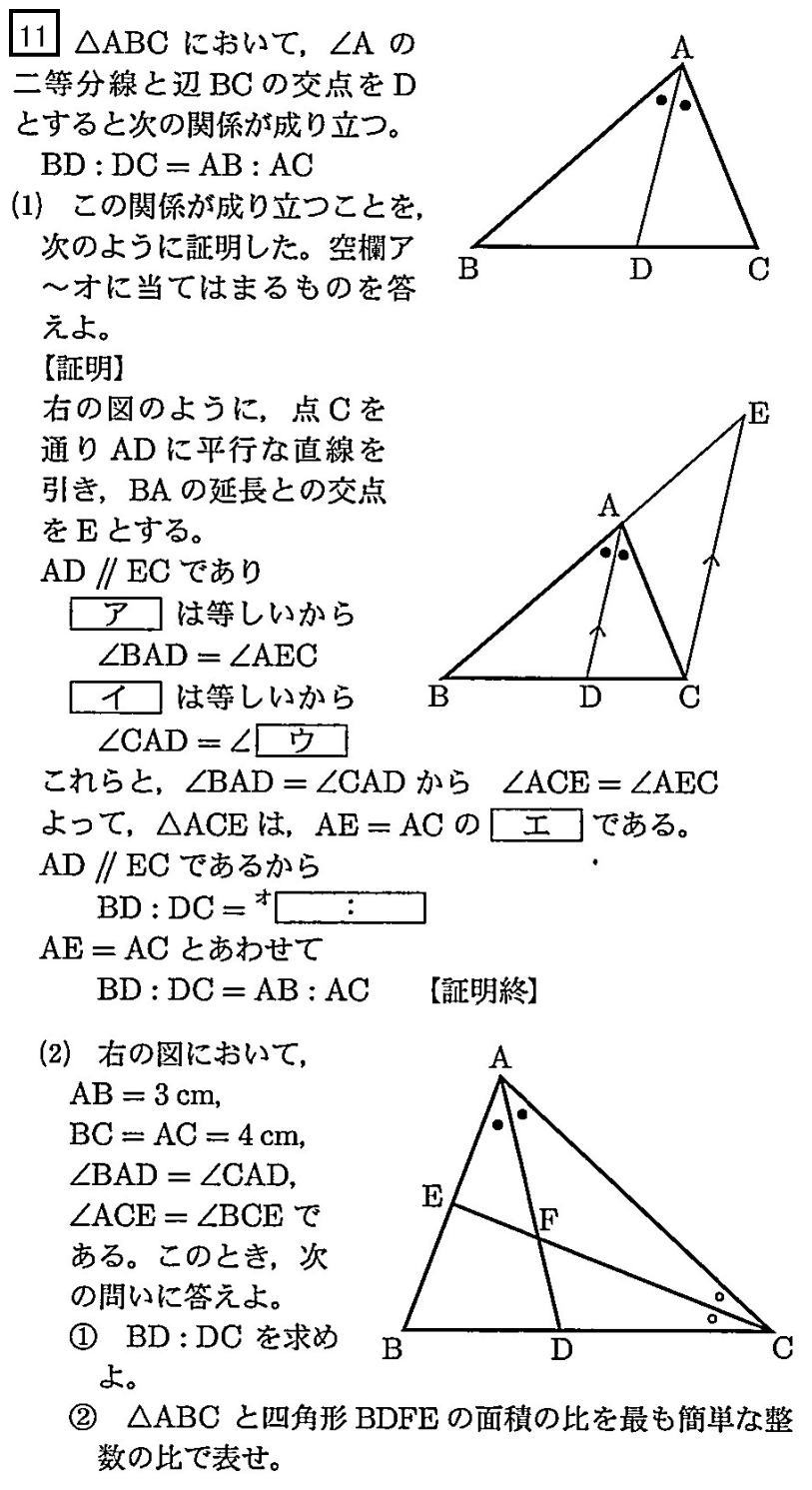
和洋国府台女子高校2022年度数学入試問題11.平面図形角の二等分線の定理(1)解説解答

（1）　BD：DC = AB：ACの関係が成り立つことを、次のように証明した。空欄ア～オに当てはまるものを答えよ。　。

解説解答



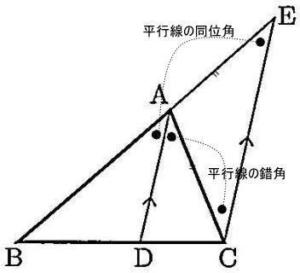
角の二等分線の定理の証明の進め方としては、相似の証明をしていきます。

角度の等しいところに着目して、二等辺三角形を発見できれば証明は完成します。

証明　

AE // ECであり、同位角は等しいから　∠BAD = ∠AEC

錯角は等しいから　∠CAD = ∠ACE

これらと、∠BAD = ∠CAD から　∠ACE = ∠AEC

よって　△ACEは　AE = ACの二等辺三角形である。

AD // ECであるから　BD：DC = BA：AE

AE = ACとあわせて　BD：DC = AB：AC 　[証明終]


答　　ア 同位角　イ　錯角　ウ　ACE　エ　二等辺三角形　オ BA：AE

和洋国府台女子高校2022年度数学入試問題11.平面図形角の二等分線の定理(1)解説解答

(2)　右の図において、AB = 3cm，BC = AC = 4cm，∠CAD = ∠CAD，∠ACE = ∠BCEである。

このとき次の問いに答えなさい。

①　BD ：DCを求めよ。

解説解答



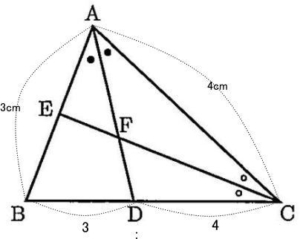
角の二等分線の定理より　AB：AC = BD：DC = 3：4


答　　　3：4

 

和洋国府台女子高校2022年度数学入試問題11.平面図形角の二等分線の定理(1)解説解答

②　△ABCと四角形BDFEの面積の比を最も簡単な整数の比で求めよ

解説解答



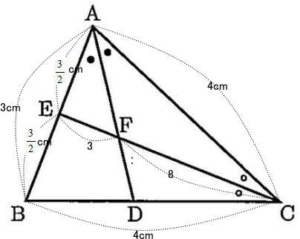
四角形BDFEの面積 = △ABDの面積 – △のAEFの面積

△ABDの面積
　AB：AC = BD：DC = 3：4

よって　△ABCの面積を1とすると



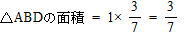
AC：BC = 4：4 = 1：1

プロ家庭教師集団スペースONEの高校受験合格のための過去問解説解答