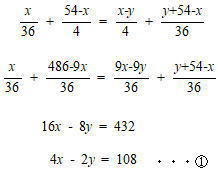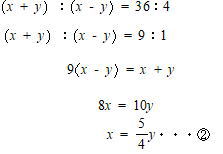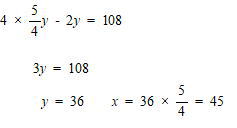早稲田実業学校高等部去問研究
2022年度早稲田実業学校高等部の数学出題構成は例年通り大問5題構成で、1.小問集合4問 2.(1)方程式の応用 (2)箱ひげ図(新教育課程で高校から中学学習へと移行) 3.座標平面 4.場合の数 5 空間図形が出題されました。
今回は 2.(1)方程式の応用をを解説します。
文章題では略図をかく等、条件を整理しましょう。プロ家庭教師集団スペースONEの高校受験合格のための過去問解説解答
早稲田大学系属早稲田実業学校高等部2022年度数学入試問題2.(1)方程式の応用 問題
2.(1) A,B2つのグループが、54km離れたP地点からQ地点に向かう。バスが1台しかなかったので、まずAグループはバスで、Bグループは徒歩でP地点を同時に出発した。
AグループはQ地点に向かう途中のR地点でバスを降り、その後徒歩でQ地点へ向かった。バスはAグループを下した後、すぐに折り返し、徒歩で移動途中だったBグループをS地点でのせて、再びQ地点に向かったところ、2つのグループは同時にQ地点に到着した。
P地点からR地点までの距離をx km、R地点からS地点までの距離をy kmとしてx とyの連立方程式をつくり、P地点からQ地点まで移動するのにかかった時間を求めよ。ただし、バスは時速36km、徒歩は時速4kmで移動するものとし、バスの降車にかかる時間は考えないものとする。早稲田大学系属早稲田実業学校高等部2022年度数学入試問題2.(1)方程式の応用 解説解答
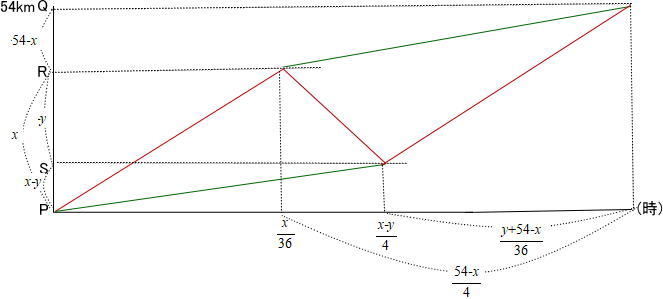
AグループがPQ間を進んだ時間とBグループがPQ間を進んだ時間は等しいので
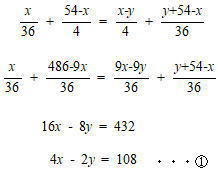
また、バスがAグル^プをのせて出発しBグループをのせるまでにかかった時間とBグループが徒歩でS地点までに進んだ時間は等しいので 速さの比 = 距離の比となる。よって
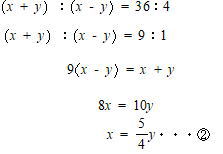
①を②に代入して
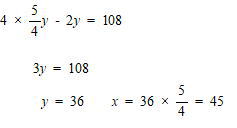
54 > x > y となり、これは問題に適する。
よって P地点からQ地点まで移動するのにかかった時間は
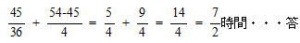
プロ家庭教師集団スペースONEの高校受験過去問解説解答