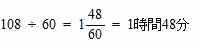芝中学・高等学校2018年度算数過去問研究
2018年度芝中学校第1回算数入試問題は 例年通りの出題構成で 1.計算2問 2.~9. 一行問題 ・大問の組み合わせでした。出題内容は1.四則計算 2.平均算 3.食塩の濃度 4.割合の問題(差が一定) 5.整数の性質 6.平面図形 7. 速さ 8.規則性 9.立体図形 でした。
解答形式も例年通り 答のみを解答欄に書く形式でした。
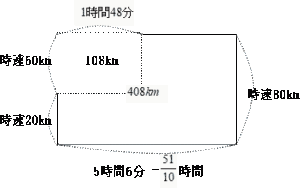
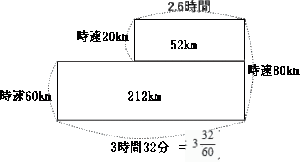
今回は 7.速さの問題を解説します。速さの鶴亀算であることがわかれば簡単に解ける問題です。
芝中学校2018年度 算数入試問題 7.旅人算 問題