武蔵中学校過去問対策

2020年度の武蔵中学校算数入試問題は、例年通りの出題構成で[1]小問2問，[2]平面図形，[3]論理・推理，[4]数の性質が出題されました。算数配点100点，合格者平均点71.9点，受験者平均点54.5点でした。

今年度の出題では[2]の平面図形は受験者にとって塾の学習でも解きなれた問題だったと思います。このような出題では[3]，[4]に時間を回す意味でも素早く解きましょう。

今回は　2.平面図形を解説します。様々な解き方が考えられますが、解法は2通りで解説しています。

武蔵中学校　2020年度算数入試問題　2.平面図形　(1)解説解答

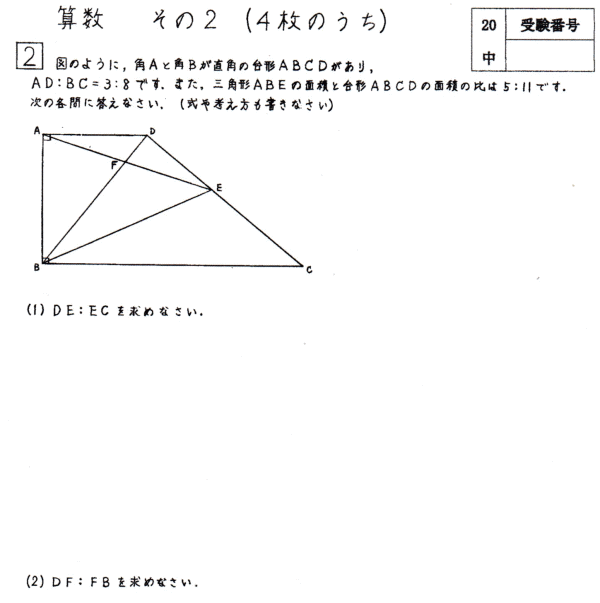
(1)　DE：ECを求めなさい。

解説解答


よって三角形ABDの面積：三角形ABEの面積：三角形ABCの面積 = 3：5：8

辺ABを底辺としたときの高さの比も3：5：8

図のように点Dから辺BCに、点Eから辺ABに垂線を引き、それぞれに交点をG，H，Iとする。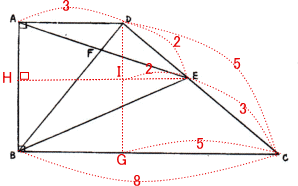

AD = HI = BG = 3　なので　IE：GC = (5 – 3)：(8 – 3) = 2：5

三角形DIEと三角形DGCは相似形なので　IE：GC = DE：DC = 2：5

したがって　DE：EC = 2：5 – 2 = 2：3

答　　　2：3

武蔵中学校　2020年度算数入試問題　2.平面図形　(1)　別解　

別解1.　変化量の割合による解法

平面上の点移動の考え方による解法です。

解説解答

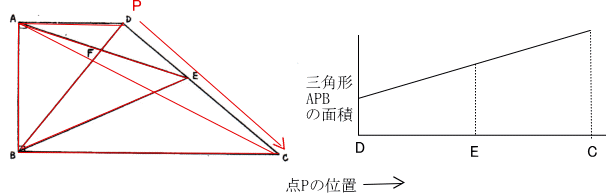
ある点Pが辺DC間を一定の速さで動くとき、三角形APBの面積は一定の割合で増えます。

三角形ABDの面積：三角形ABEの面積：三角形ABCの面積 = 3：5：8なので

DE：EC = (5-3)：(8 – 5) = 2：3

答え　　2：3


別解2.　高さABの長さが等しいことから、底辺の比 = 面積比を用いた解法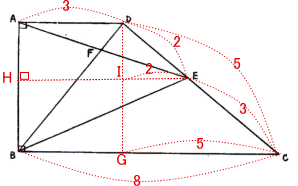



台形ABCDの底辺= (AD + BC)，三角形ABDの底辺 = AD，三角形ABEの底辺 = HE，三角形ABCの底辺=BC

よって　(5 – 3)：(8 – 5) = 2：3

答え　　2：3

武蔵中学校　2020年度算数入試問題3.平面図形　(2)　解説解答

(2)　DF：FBを求めなさい。

解説解答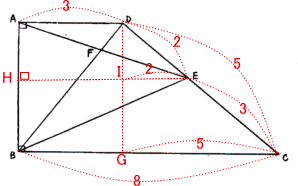



AEを底辺とするとき　三角形AEDと三角形ABEの面積比は　三角形AEDと三角形ABEの高さの比と同じになる。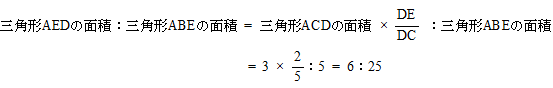



答え　　6：25