MENU

記事の作成者：プロ家庭教師集団スペースONEとは

最新情報

  • HOME
    •  > 
  • 過去問対策
    •  > 
  • 渋谷教育学園幕張中学校2022年度算数入試問題1.規則性

    • 2022/04/01

    • 中
    • オ
    • 過去問対策

    渋谷教育学園幕張中学校2022年度算数入試問題1.規則性

    渋谷教育学園幕張中学校算数過去問研究


    2022年度渋谷教育学園幕張中学校第１回入学試験は、募集人数　男女共学　約215名に対し　応募者男子1281名　女子640名　受験者男子1208名　女子589名　合格者男子461名　女子190名。

    教科別入試結果は　国語受験者平均点56.5点　合格者平均点64.9点　合格者最低点35点　算数受験者平均点52.0点　合格者平均点64.0点　合格者最低点28点　社会受験者平均点44.5点　合格者最平均点49.4点　合格者最低点23点　理科受験者平均点62.8点　合格者平均点50.3点　合格者最低点24点　合格者最低点209点　合格者最低得点率　59.7%でした。

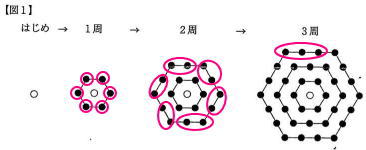
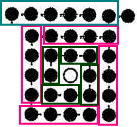
    算数入試問題は、例年通り小問集合のない大問5題構成で、出題内容は1.規則性　2.場合の数　3.速さ　4.平面図形　5.立体図形でした。

    今回は　1.規則性を解説します。

     

    渋谷教育学園幕張中学校2022年度算数入試問題1.規則性　問題


     

     

    渋谷教育学園幕張中学校2022年度算数入試問題1.規則性(1)解説解答　

    (1)　初めの白石をちょうど10周まで黒石で囲むために必要な石の総数は、はじめの白石を含めて何個ですか。

    解説解答



    １周目の黒石の数は　1×6 ≒6個

    2周目の黒石の数は　2×6 ≒12個

    3周目の黒石の数は　3×6 ≒18個・・・

    よって　10周目までの黒石の数は　

    1×6 + 2×6 + 3×6 + ・・・・・10×6 = ( 1+2+3+・・・10)×6

    　　　　　　　　　　　　　　　　　　　= (1 + 10)×10÷2×6

    　　　　　　　　　　　　　　　　　　　= 330

    はじめの白石を含めて331個


    答　　　　331個

     

     

    渋谷教育学園幕張中学校2022年度算数入試問題1.規則性　(2)解説解答

    (2)　黒石の総数が1000個のとき、はじめの白石を最大で何個まで黒石で囲むことができますか。

    解説解答


    　
    (1)より　□周目までの黒石の数は　

    1×6 + 2×6 + 3×6 + ・・・・・□×6 ＜ 1000

    1000÷6 = 166.6・・・

    1から　15までの和は　(1 + 15)×15÷2 = 120

    1から　16までの和は　120 + 16 = 136

    1から17までの和は　136 + 17 = 152

    1から18までの和は　152 + 18 = 170

    したがって　17周まで


    答　　17周

     

     

    渋谷教育学園幕張中学校2022年度算数入試問題1.規則性(3)解説解答　

    (3)　まず　[図1]のように、はじめの白石をちょうど□周まで囲むように黒石を置きました。次に、そこで用いた黒石を全て使って[図2]のように、はじめの白石を正方形で囲むように置き直したところ、ちょうど何周かの正方形で囲むことができました。□に入る最も小さい数を求めなさい。

    解説解答

    図1の並べ方は　(1 + 2 +・・・+ □)×6

    [図2]のように、はじめの白石を正方形で囲むように置き直したら



    図の通り　1周目は　(3 – 1)×4 = 2×4 = 8個で囲む。

    1周目は　(5-1)×4 = 4×4 =16個で囲む。

    1辺に2個ずつ増えていくので、6×4 = 24

    1周目 + 2周目 + 3周目= (2 + 4 + 6) ×4 = 2×(1 + 2 + 3) = (1 + 2 + 3)×8 = 48

    よって　図2の並べ方だと、黒石の総数個は(1 + 2 + ・・・+ □) ×8

    図1 ( 1 + 2 + 3 +・・・+ □)×6

    図2(1 + 2 + 3 + ・・・+ □) ×8

    ( 1 + 2 + 3 +・・・+ □)×6 = (1 + 2 + 3 + ・・・+ □) ×8

    図1 ( 1 + 2 + 3 +・・・+ □)×6 = 1 + 2 + 3 +・・・+ □)×2×3

    図2(1 + 2 + 3 + ・・・+ □) ×8 1 + 2 + 3 +・・・+ □)×2×4

    ( 1 + 2 + 3 +・・・+ □)×2×3 = (1 + 2 + 3 + ・・・+ □) ×2×4

    よって　図1と図2は　3の倍数 = 4の倍数なので　逆比より

    図1　 (1 + 2 + 3 + ・・・+ □) =4の倍数
    図2 　(1 + 2 + 3 + ・・・+ □) =3の倍数


    1 + 2 + 3 +・・・+ □　が　4の倍数となるときを考えると

    1，3，6，10，15，21，28

    28 ÷4 = 7　よって　1 + 2 + 3 + 4 + 5 + 6 + 7= 28 　なので　7周

    また　1 + 2 + 3 +・・・+ □　が　3の倍数となるときを考えると

    1，3，6，10，15，21

    21 ÷3 = 7　


    答　　　7周
    合格者お喜びの声はこちら

    各種お問い合わせにつきましては、下記よりお気楽にお問い合わせください。

    お問い合わせはこちら
    メールでお問い合わせ
    LINEでお問い合わせ

    オンライン家庭教師も在籍中！「お問い合わせ種別」の欄を選択ください。

    営業時間：AM 10:00 〜PM 9:00