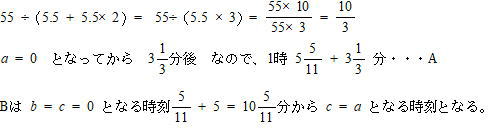開成学園　開成中学校過去問対策

2022年度開成中学入学試験は、出願者1206名　受験者1050名　合格者416名でした。

科目ごとの入試結果は　国語合格者平均点45.6点　受験者平均点 38.8点　算数合格者平均点60.7点　受験者平均点50.7点　理科合格者平均点54.0点　受験者平均点48.6点　社会合格者平均点54.6点　受験者平均点51.0点でした。

2022年度の開成中学校算数入試問題は、[1]小問集合4問　[2]立体図形　[3]場合の数　[4]時計算が出題されました。

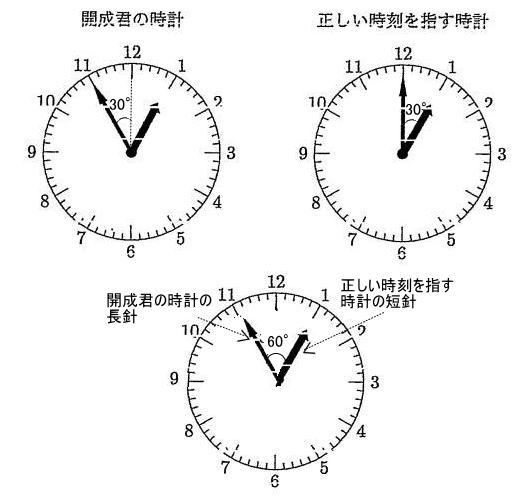
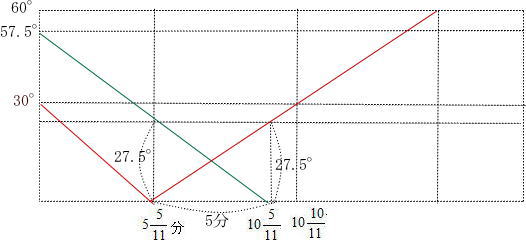
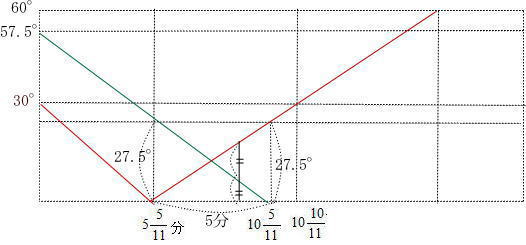
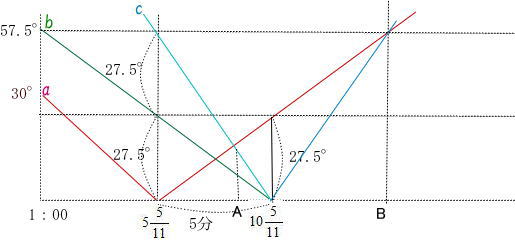
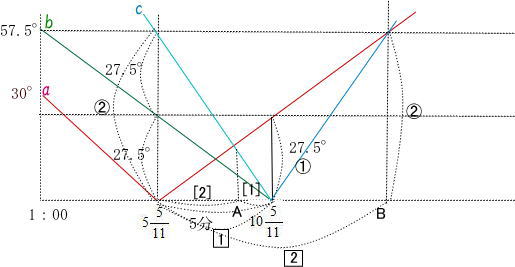
今回は[4]時計算を解説します。時計算は　スペースONEプロ家庭教師が2010年度，2014年度の開成中学の時計算を解説しています。

(1)は基本問題　(2)(3)が応用問題です。頻出問題は過去問を通して十分対策をとりましょう。


2010年度開成中学算数入試問題3.時計算解説解答へ

2014年度開成中学算数入試問題時計算解説解答へ

プロ家庭教師集団スペースONEの開成中学合格のための過去問対策へ

プロ家庭教師集団スペースONEの中学受験過去問対策へ

開成中学校2022年度算数入試問題4.時計算(3)　別解相似比と速さの比で解く解説解答

(3)　正しい時刻で1時を過ぎたあと、(1)の時刻までの間で、aがbの2倍になる時刻をAとし、(1)の時刻を過ぎてから初めてaがbの2倍になる時刻をBとします。時刻Aから時刻Bまでの時間は何分何秒ですか。

解説解答

下図のように a = 0のとき、aとbの角の差の2倍となる点Cをとる。角度が2倍となるので、短針と長針の動く速さも2倍として考える。