開成学園 開成中学校過去問研究
2010年度開成中入試問題の算数は大問が4題から3題に減り、例年より易しくなっています。
算数の合格者平均点もここ数年の中では一番高いようです。
3番の(2)が開成中らしい考えさせる問題ですが、他の問題を完答すれば合格者平均点に達するでしょう。
算数入試問題 (時計算にチャレンジ)
開成中学校2010年度算数入試問題3.時計算 問題
| 問題 | |
| 10時10分から11時10分までの60分間の時計の時針(短針)、分針(長針)、秒針について、次の問に答えなさい。 (1) 時針と分針の重なる時刻を求めなさい。ただし、秒の値のみ分数を用いて答えること。 | |
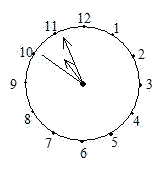
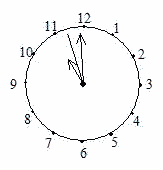
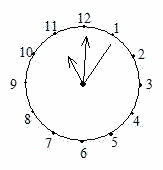
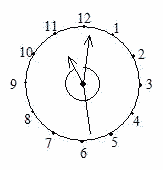
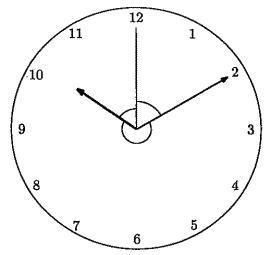
| (2) 時針、分針、秒針の3つの針が、どの2つも重なっていないときを考えます。 このとき、右の図のように時計の中心は3つの角に分かれます。 (1)で求めた時刻から11時10分までの間に、このうち2つの角が等しくなる回数と、最後に2つの角が等しくなる時刻を求めなさい。 ただし、時刻については秒の値のみ分数を用いて答えること。 | |
 | |
開成中学校2010年度 算数入試問題3.時計算 解説解答
| 10時10分から11時10分までの60分間の時計の時針(短針)、分針(長針)、秒針について、次の問に答えなさい。 (1) 解説解答 | |||||||||||||||||||||||
| (1) 時針と分針の重なる時刻を求めなさい。ただし、秒の値のみ分数を用いて答えること。 | |||||||||||||||||||||||
| 解説解答 | |||||||||||||||||||||||
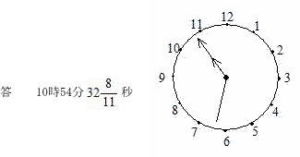
| (1) 時計算の重なりの基本的な問題です。秒針まで求めるので計算に注意しましょう。 | |||||||||||||||||||||||
| 10時の時、時針と分針は300度離れています。分針は時針に毎分5.5度近づくので | |||||||||||||||||||||||
 | |||||||||||||||||||||||
(2) 解説解答 | |||||||||||||||||||||||
| (2) 時針、分針、秒針の3つの針が、どの2つも重なっていないときを考えます。 このとき、右の図のように時計の中心は3つの角に分かれます。 (1)で求めた時刻から11時10分までの間に、このうち2つの角が等しくなる回数と、最後に2つの角が等しくなる時刻を求めなさい。 ただし、時刻については秒の値のみ分数を用いて答えること。 | |||||||||||||||||||||||
| 解説 | |||||||||||||||||||||||
| (2)三つの針でできる角度のうち二つの角が等しくなる場合は四通りあります。 | |||||||||||||||||||||||
| |||||||||||||||||||||||