第1回入試結果は、受験者平均点 国語68.1点 算数58.8点 理科24.3点 社会34.3点でした。
2022年度 浦和明の星女子中学校算数入試問題
2022年度第1回浦和明けの星女子中学校算数入試問題は、1.小問集合7問 2.速さ(ダイヤグラム) 3.水槽算 4.平面図形の移動(図形の重なり) 5.論理・推理が出題されました。
今回は1.小問集合を解説します。計算が煩雑です。手早く解けるよう日ごろから練習をしましょう。
記事の作成者:プロ家庭教師集団スペースONEとは
浦和明の星女子中学校2022年度算数入試問題1.小問集合
2022年度 浦和明の星女子中学校算数入試問題
2022年度第1回浦和明けの星女子中学校算数入試問題は、1.小問集合7問 2.速さ(ダイヤグラム) 3.水槽算 4.平面図形の移動(図形の重なり) 5.論理・推理が出題されました。
今回は1.小問集合を解説します。計算が煩雑です。手早く解けるよう日ごろから練習をしましょう。

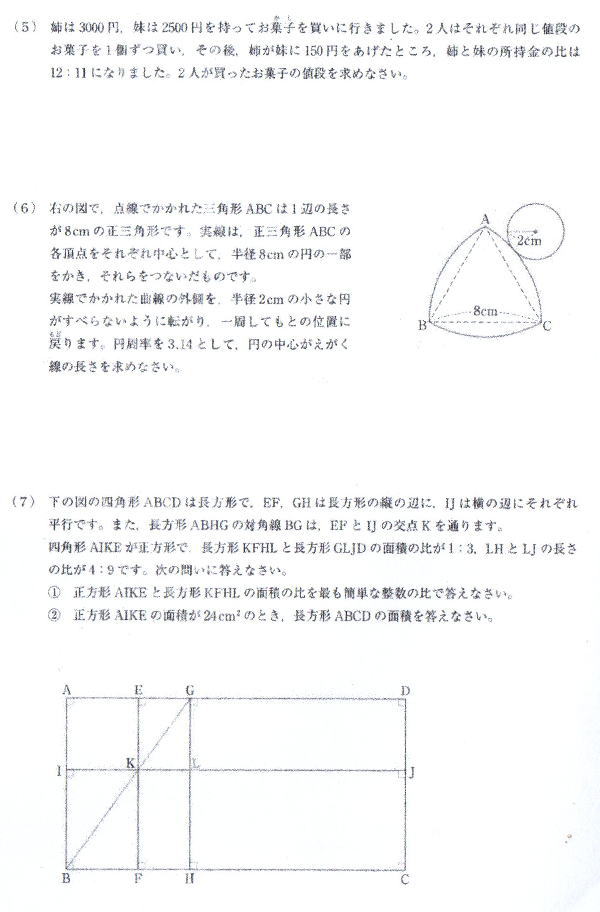

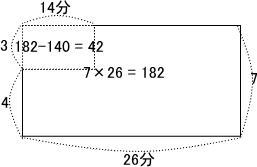
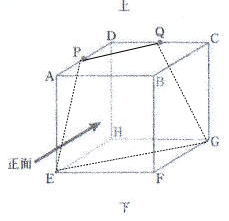
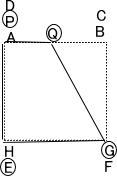
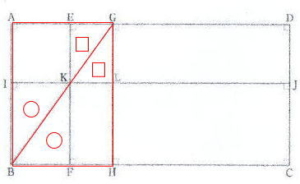
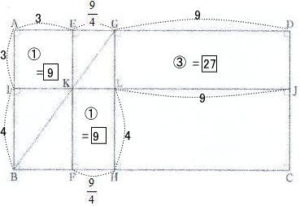

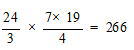
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00