東京都立立川高等学校数学過去問研究
都立立川高校2021年度自校作成数学問題は例年通り大問4題構成ですが例年出題されていた4.空間図形に代わり平面図形とブロックとの融合問題が出出されました。
2021年度数学出題問題1.小問集合5問 2.関数のグラフ 3.平面図形 4.平面図形とブロックの融合問題の中から 今回は3.平面図形を解説します。作図や証明問題は過去問を繰り返して本番に備えましょう。
記事の作成者:プロ家庭教師集団スペースONEとは
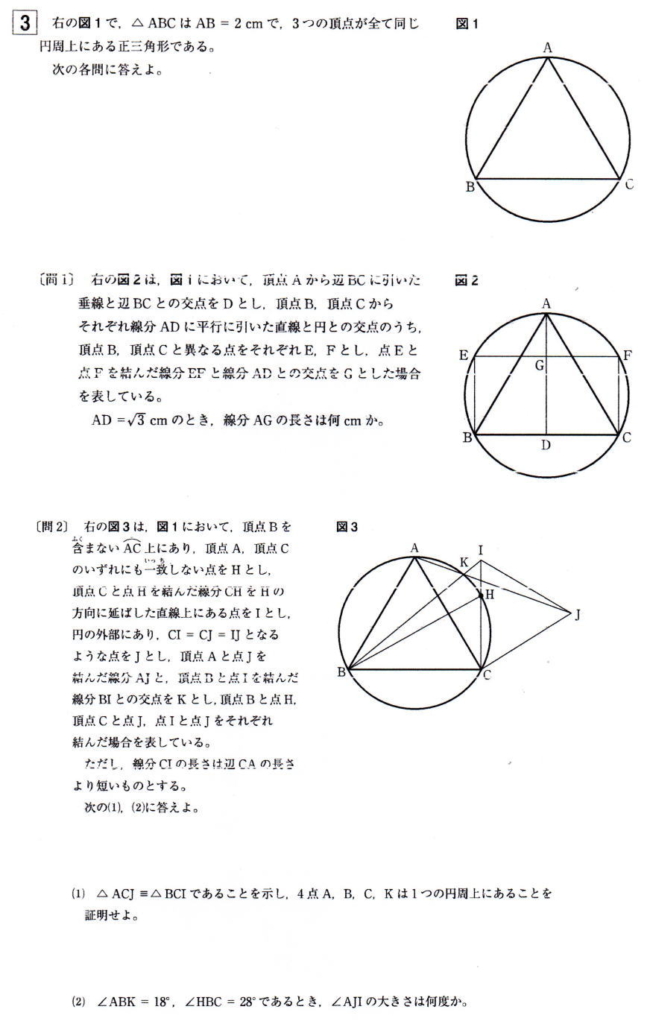
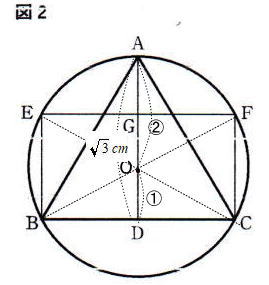
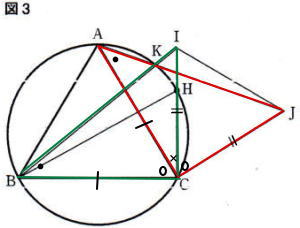
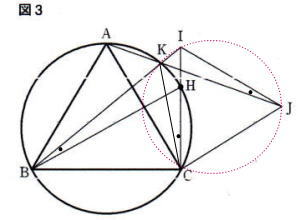
東京都立立川高校2021年度自校作成数学考査問題3.平面図形
都立立川高校2021年度自校作成数学問題は例年通り大問4題構成ですが例年出題されていた4.空間図形に代わり平面図形とブロックとの融合問題が出出されました。
2021年度数学出題問題1.小問集合5問 2.関数のグラフ 3.平面図形 4.平面図形とブロックの融合問題の中から 今回は3.平面図形を解説します。作図や証明問題は過去問を繰り返して本番に備えましょう。
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00