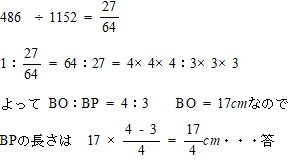2020年度桜美林高校第2回数学入試問題は1.小問集合11問,2.関数とグラフ,3.平面図形 4.割合の文章題(体積)が出題されました。
今回は 4.割合の文章題を解説します。浮力の問題ですが、課題文中に浮力についての解説があります。誘導に従って計算しましょう。(3)は体積比を用いて計算しましょう。
桜美林高校2020年度 第2回数学入試問題 4. 割合 問題
桜美林高校2020年度 第2回数学入試問題 4. 割合 (1) 解説解答
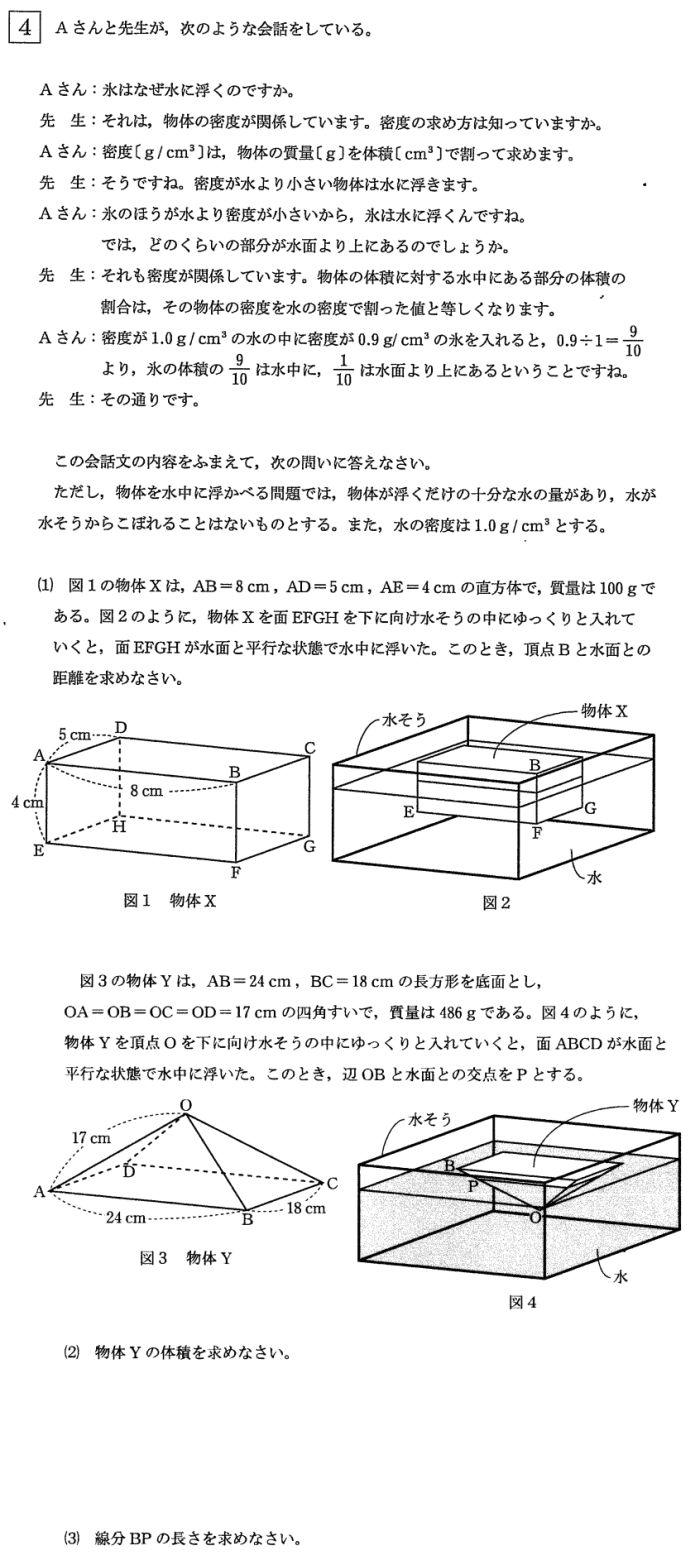
(1) 図1の物体Xは、AB = 8cm,AD = 5cm,AE = 4cmの直方体で、質量は100gである。図2のように、物体Xを麺EFGHを下に向け水そうの中にゆっくりと入れていくと、麺EFGHが水面と平行な状態で水中に浮いた。このとき、頂点Bと水面との距離を求めなさい。
解説解答
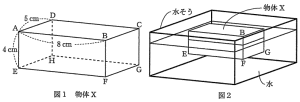
物体Xの体積は 5×8×4 = 160c㎥
物体Xの密度は Aさんの答え「密度(g/c㎥) は物体の質量(g)を体積で割って求めます。」より
解説解答

物体Xの体積は 5×8×4 = 160c㎥
物体Xの密度は Aさんの答え「密度(g/c㎥) は物体の質量(g)を体積で割って求めます。」より
物体Xの体積に対する水中にある部分の体積の割合は 先生の説明から「その物体の密度を水の密度で割った値と等しくなる」ので
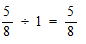
よって 水面より上にある物体Xの割合は
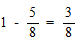
したがって 頂点Bと水面との距離は
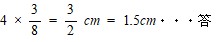
桜美林高校2020年度 第2回数学入試問題 4. 割合(2) 解説解答
よって 水面より上にある物体Xの割合は
したがって 頂点Bと水面との距離は
桜美林高校2020年度 第2回数学入試問題 4. 割合(2) 解説解答
解説解答
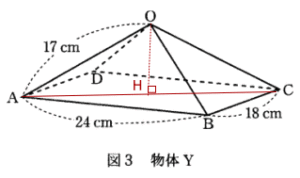
三平方の定理より
ACの中点をHとすると、AH = 15cm
∠OHA = 90°なので
したがって 物体Yの体積は
桜美林高校2020年度 第2回数学入試問題 4. 割合(3) 解説解答
(3) 線分BPの長さを求めなさい。
解説解答
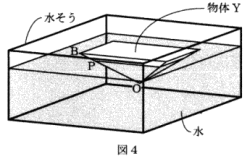
物体Yの体積は1152c㎥,質量は486g, 水の密度は1なので、物体Yの密度も水中にある部分の体積の割合も