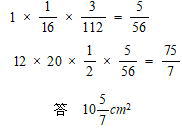鴎友学園女子中学校算数過去問研究
2011年度鴎友学園女子中学校算数第1回入試問題は 例年通りの出題構成で、1.~3.一行問題 4.~8 大問(枝問各2~3)。
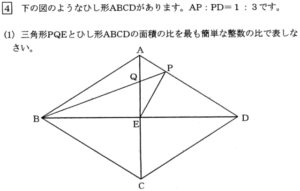
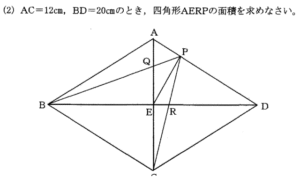
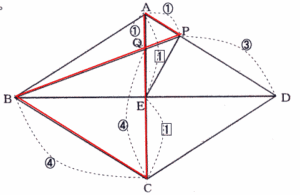
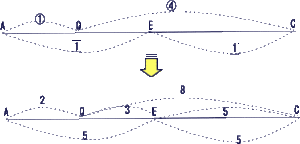
出題内容は、1.割合の文章題 2.売買損益 3. 倍数変化算 4.平面図形(ひし形) 5.回転図形 6.平面上の点移動 7.立体図形の抜き取り 8. 水槽のグラフ でした。
総解答箇所12.試験時間は50分。配点は100点でした。
第1回算数受験者最高点は94点,合格者平均点は64.4点てした。
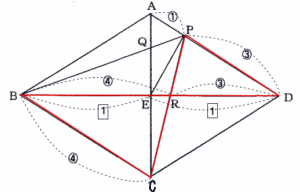
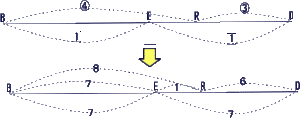
今回は 4.平面図形(ひし形)を解説します。