立教女学院中学校過去問研究
20013年度立教女学院中学校算数入試問題は例年通り 1.四則計算を含む小問集合8問 2.二等辺三角形の回転図形 3.約束記号 4.平面上の点移動(グラフの読み取り)の大問4問構成でした。解答も答のみを解答欄に書き込む形式でした。
今回は4を解説します。
4は文意を読み取って四角形を自分で作図することによって解ける問題です。
記事の作成者:プロ家庭教師集団スペースONEとは
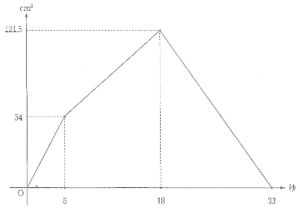
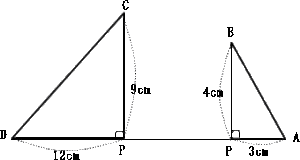
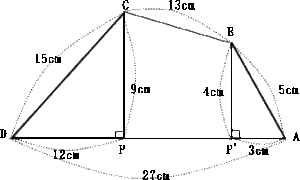
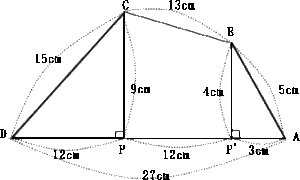
立教女学院中学校2013年度算数入試問題4.平面上の点移動
20013年度立教女学院中学校算数入試問題は例年通り 1.四則計算を含む小問集合8問 2.二等辺三角形の回転図形 3.約束記号 4.平面上の点移動(グラフの読み取り)の大問4問構成でした。解答も答のみを解答欄に書き込む形式でした。
今回は4を解説します。
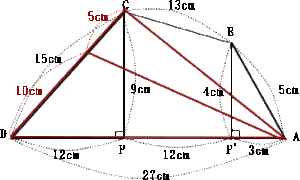
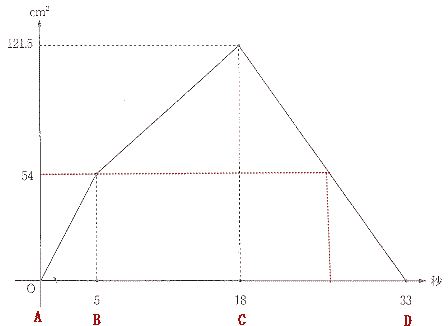
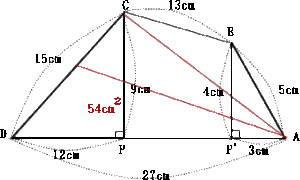
4は文意を読み取って四角形を自分で作図することによって解ける問題です。


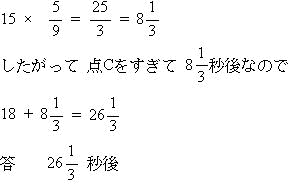
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00