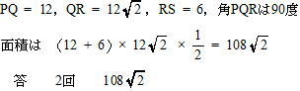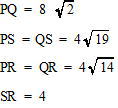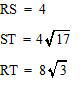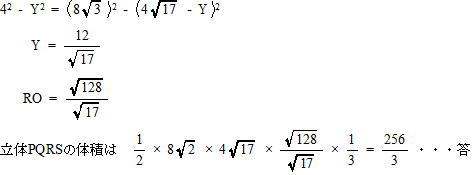都立戸山高校過去問傾向と対策2020年度数学入試問題4.立体上の点移動 |プロ家庭教師集団スペースONE【公式】

東京都立戸山高等学校過去問対策

都立戸山高校はスーパーサイエンスハイスクール指定校です。多くの進学校が2学期制　45分 7時間授業を進める中、戸山高校は3学期制50分6時間授業を続けており、3年まで文理分けをせず、すべての生徒が共通で文理の科目を学びます。また自由な校風が電灯であることから制服のない私服校です。東京都立戸山高校2020年度数学入試問題は、例年通り大問4題構成で、1.小問集合
2.関数 3.平面図形(円の性質) 4.立体上の点移動　が出題されました。

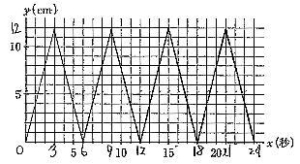
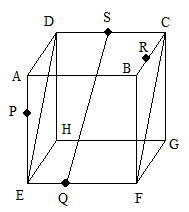
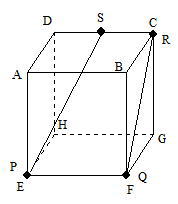
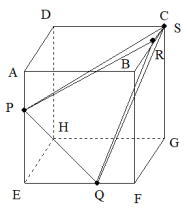
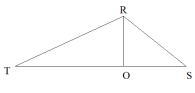
今回は　4.立体上の点移動を解説します。問1は基本　問2.3が難問でした。戸山高校を志望する受験生は　問2，3レベルの問題を他の進学重点校の過去問でも繰り返し練習しましょう。　　　

都立戸山高校2020年度数学入試問題4.立体上の点移動　問題

都立戸山高校2020年度数学入試問題4.立体上の点移動　(1)　解説解答

問1　次の(1)(2)に答えよ。

解説解答

　点PはEA間を毎秒4cmの速さで動くので、Eを出発し　12÷4 = 3秒後にAに着く。同様に3秒ごとにE→A→E・・・と動いていく。

答

都立戸山高校2020年度数学入試問題4.立体上の点移動　(2)　解説解答

この問題は問1のようにｘを使って考える問題ではありません。発想を変えます。
線分SQは常に平面CDEF上にあります。

P、Rが上図のような位置にあるとき、線分PRは平面CDEFと交わることはありません。

つまり4点では四角形はできません。

線分PRが平面CDEF 上にあるのは点Pが点E、点Rが点Cにある時だけです。

そうなるときの時間を求めます。

点Pが点Eにくる時　0秒、6秒、12秒、18秒、24秒点Rが点Cにくる時　6秒、18秒

点Sが点Cにくる時　4秒、12秒、20秒、

点Qが点Eにくる時　0秒、12秒、24秒

　点P、,点Rが点E、点Cに同時にくるのは、6秒と18秒の2回あることがわかります。またその時は点S、点Qと重なることはありません。

はじめて4点で四角形になるときは6秒後下図のような台形になります。