中央大学付属高等学校過去問研究
中央大学付属高等学校の2008年度数学一般入試問題は計算・小問６題を含む大問５題構成でした。
標準問題が中心ですが、思考力を求める問題が含まれています。上級レベルの問題にも積極的に取り組みましょう。
中央大学附属高校2008年度 一般数学入試問題 問5 立体図形 問題
図のように AB=4ｃｍ、AD=3ｃｍ、AE=15ｃｍの直方体ABCD-EFGHを点Eを通る平面で２つの立体に分けた。
その切り口は、四角形EPQRである。
FP=5ｃｍ、GQ=12ｃｍのとき、次の問いに答えなさい。
（１）HRの長さを求めなさい。
（２）EQの長さを求めなさい。
（３）頂点Gを含むほうの立体の体積を求めなさい。
（４）２つの立体の表面積の差を求めなさい。
解説解答
(1) 解説解答
（１）HRの長さを求めなさい。
解説解答
点Ｒから辺ＣＧに垂線ＲＩをおろすと、
△EPFと△RQIにおいて、QR//PE, なので、
QR=EP, RI=EF, ∠QRI＝∠PEF
よって △EPF≡△RQI
QI=5ｃｍなので
RH＝IG＝１２－５＝７
答 ７ｃｍ
答 ７ｃｍ
（２）EQの長さを求めなさい。
解説解答
ＥＧ2＝42＋32
ＥＧ＝5
ＥＱ2＝52＋122
ＥＱ＝13
答 13ｃｍ
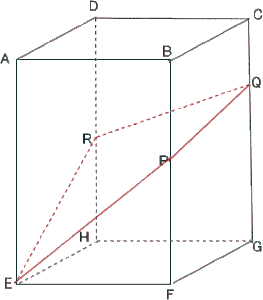
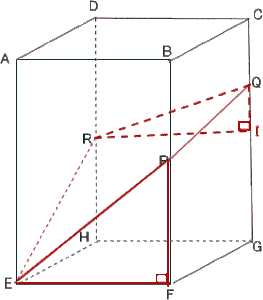
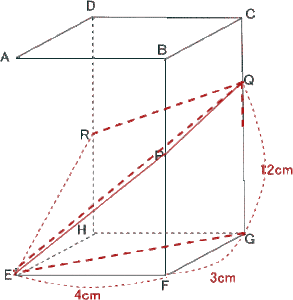
(３) 解説解答
（３）頂点Gを含むほうの立体の体積を求めなさい。
解説解答
点Ｑを通り底面に平行な平面で立体を切り取ると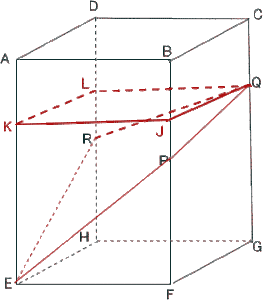
平面ＥＰＱＲによって直方体ＫＬＱＪ－ＥＨＧＦは合同な立体に分けられるので、
３×４×１２÷２＝７２
答 ７２㎤
答 ７２㎤
(４) 解説解答
（４）２つの立体の表面積の差を求めなさい。
解説解答
2つの立体の表面積の差は斜線部分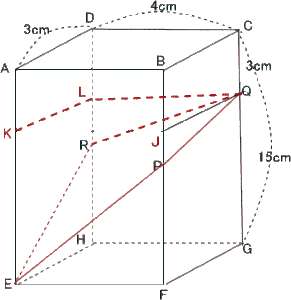
（３×２＋４×２）×３＝４２
答 ４２ｃ㎡