成城高等学校過去問研究
昨年同様大問9題の出題構成，[1]～[5]は計算を含む一行問題。[6]確率，[7]関数，[8]円の性質，[9]立体図形が出題されました。数学の配点は100点，受験者平均点37.4点，合格者平均点46.4点，合格者最高点88点，合格者最低点12点でした。
今回は8 円の性質を解説します。
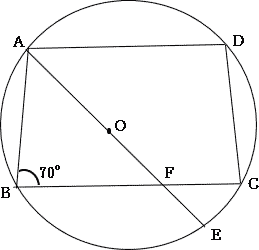
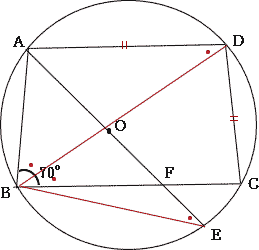
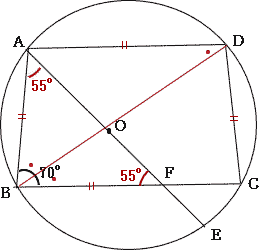
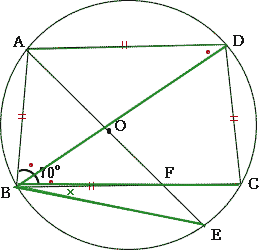
円に内接する四角形の性質，円周角の性質，三平方の性質を用いる標準レベルの問題です。補助線を適宜利用して解いていきましょう。
成城高校 2014年度 数学入試問題 8. 円に内接する四角形の問題
AEは直径で∠ABC = 70°のとき
(1) ∠BAEの大きさは[ソ]°である。
(2) 線分BFの長さは[タ]cmである。
(3) 弧ABと弧CEの長さの比は[チ]：[ツ]である。
(1) 解説解答
(1) ∠BAEの大きさは[ソ]°である。
解説
点Bと点D，点Bと点Eをそれぞれ直線で結ぶ。
AD = DCなので弧AD = 弧DCより∠ABE = ∠DBC = 35°
AD//BCなので、∠DBC = ∠ADB = 35°(錯覚)
また△FBEにおいて、
∠FBE = ∠ABE – ∠ABC
∠ABE = 90°(直径の円周角)なので
∠FBE = 90°- 70°= 20°・・・①
∠FEB = ∠ADB = 35°(弧ABの円周角)・・・②
①，②より
∠BAE = ∠FBE + ∠FEB = 35°+ 20°= 55°
答 55°
解説
点Bと点D，点Bと点Eをそれぞれ直線で結ぶ。
AD = DCなので弧AD = 弧DCより∠ABE = ∠DBC = 35°
AD//BCなので、∠DBC = ∠ADB = 35°(錯覚)
また△FBEにおいて、
∠FBE = ∠ABE – ∠ABC
∠ABE = 90°(直径の円周角)なので
∠FBE = 90°- 70°= 20°・・・①
∠FEB = ∠ADB = 35°(弧ABの円周角)・・・②
①，②より
∠BAE = ∠FBE + ∠FEB = 35°+ 20°= 55°
答 55°
(2) 解説解答
解説
(1)より ∠ABD = ∠ADB より底角が等しいので△ABDはAB = AD = 6cm の二等辺三角形
また、 ∠BAF = 180°- (70°+ 55°) = 55°底角が等しいので △ABFはAB = FBの二等辺三角形
したがってAB = AD = FB = 6cm
答 6cm
(3) 解説解答
(3) 弧ABと弧CEの長さの比は[チ]：[ツ]である。
解説
弧ABと弧CEの長さの比 = 弧ABと弧CEの円周角の比なので、弧ABの円周角∠ADBと弧CEの円周角∠CBEを求めるとよい。
(1)より ∠ADB = 35°，
また、∠ABE = 90°(直径の円周角)なので∠CBE = 90°- 70°= 20°
35：20 = 7：4
答 7：4