成蹊中学高等学校算数入試問題傾向と対策
成蹊中学校2008年度算数入試問題
(速さの出会いと追いかけにチャレンジ)
記事の作成者:プロ家庭教師集団スペースONEとは
成蹊中学校傾向と対策2008年度算数入試問題3.速さの出会いと追いかけ
成蹊中学校2008年度算数入試問題
(速さの出会いと追いかけにチャレンジ)
3. 太郎君はA町を、次郎君はB町を午前7時に、同時に出発し、太郎君は自転車でB町に向かい、次郎君は時速5kmの速さで歩いてA町に向かいました。
太郎君と次郎君は午前8時12分に初めて出会い、その後、太郎君はB町に着いて直ちに折り返し、それまでと同じ速さで次郎君を追いかけたところ、午前9時ちょうどに次郎君に追いつきました。
太郎君の自転車の速さは時速何kmですか。
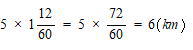
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00