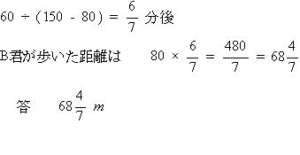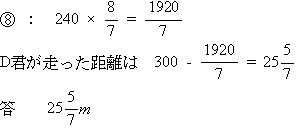桜蔭学園 桜蔭中学校高等学校過去問対策研究
2015年度桜蔭中学校入学試験は出願者655名 受験者625名 合格者271名 補欠合格者28名でした。
算数入試問題は昨年同様の問題構成で、昨年の規則性に偏った出題ではなく、全範囲から満遍なく出題されていました。
出題構成も例年通り小問も四則計算2を含む小問3問と大問4問で、四則計算以外は考え方を書く解答形式でした。
出題内容はⅠ.計算2問と小問1問 Ⅱ.平面の(うずまき状に配置した三角形) Ⅲ.文章題(場合の数) Ⅳ.立体図形 Ⅴ.速さ(追いかけ算応用)でした。
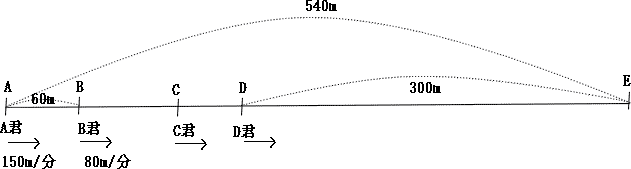
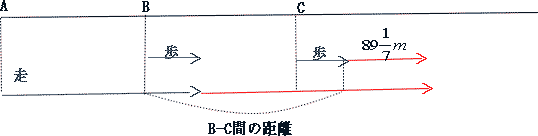
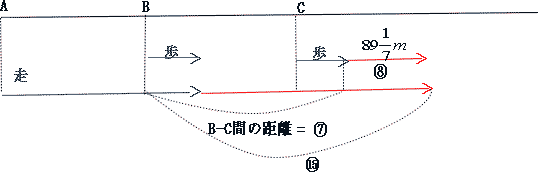
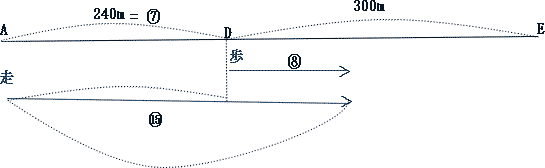
今回はⅤ.速さ(追いかけ算応用)を解説します。
算数入試問題 Ⅴ.速さ(追いかけ算応用にチャレンジ)