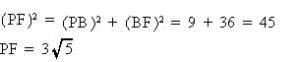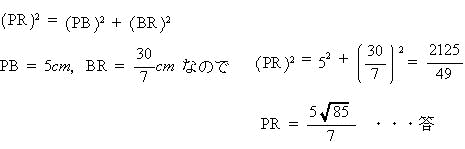慶應義塾高等学校過去問研究
2012年度慶應義塾高校数学入試問題は、昨年度より 小問が減り 大問が1題増えましたが、全体のボリュームは例年通りでした。
出題内容は 1.小問集合4問 2.平面図形の対象軸と回転図形 3.二次関数のグラフ 4.約束記号 5.連立方程式の解 6.円の性質 7.立方体上の点移動と図形の分割でした。
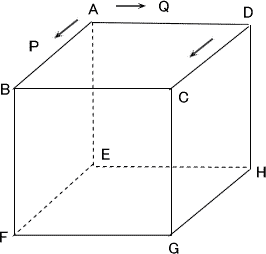
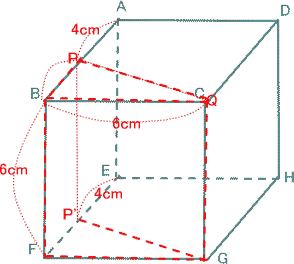
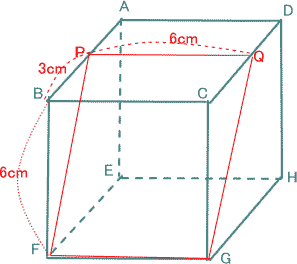
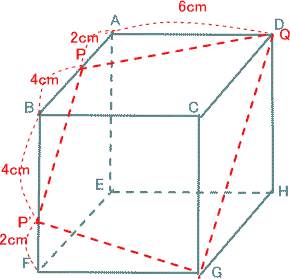
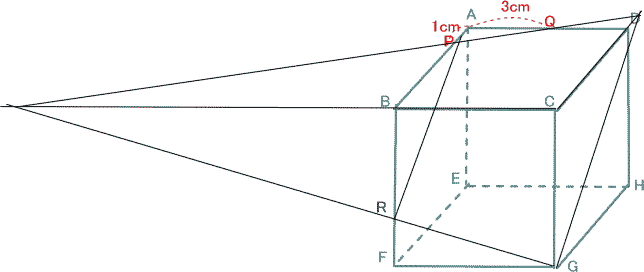
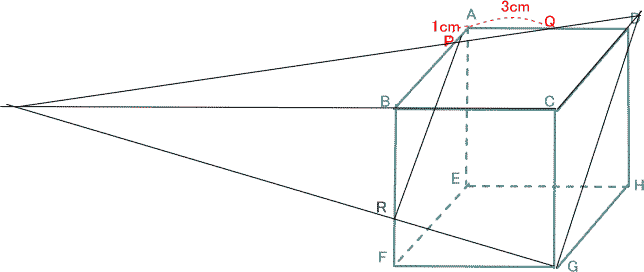
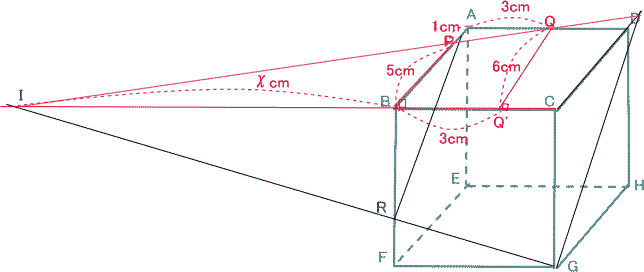
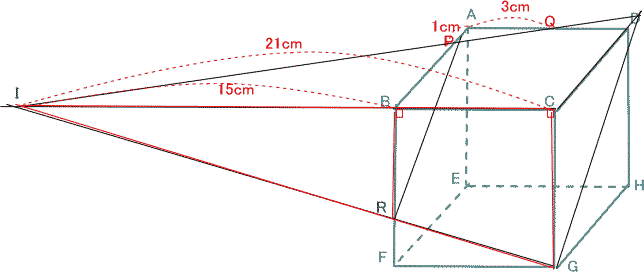
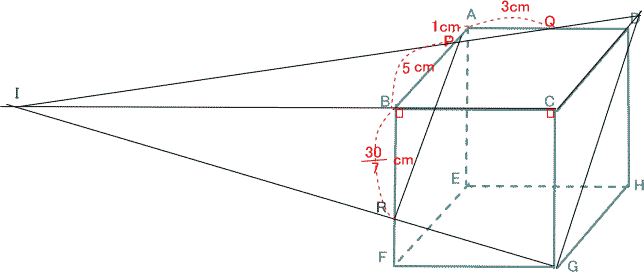
今回は 慶應義塾高校数学頻出問題 7.立方体上の点移動と図形の分割を解説します。
出題内容は 1.小問集合4問 2.平面図形の対象軸と回転図形 3.二次関数のグラフ 4.約束記号 5.連立方程式の解 6.円の性質 7.立方体上の点移動と図形の分割でした。
今回は 慶應義塾高校数学頻出問題 7.立方体上の点移動と図形の分割を解説します。