海城学園 海城中学校入試算数過去問研究
平面上の点移動によってできる三角形の面積は移動する点がどの位置にあるかをグラフの折り方によって考えていきます。数多く類題を解くことによって、すぐ解きのコツがつかめます。
海城中学の2015年度の入試問題から4.の平面上の点移動を解説解答します。
海城中学校2015年度1日目算数入試問題4.平面上の点移動 問題
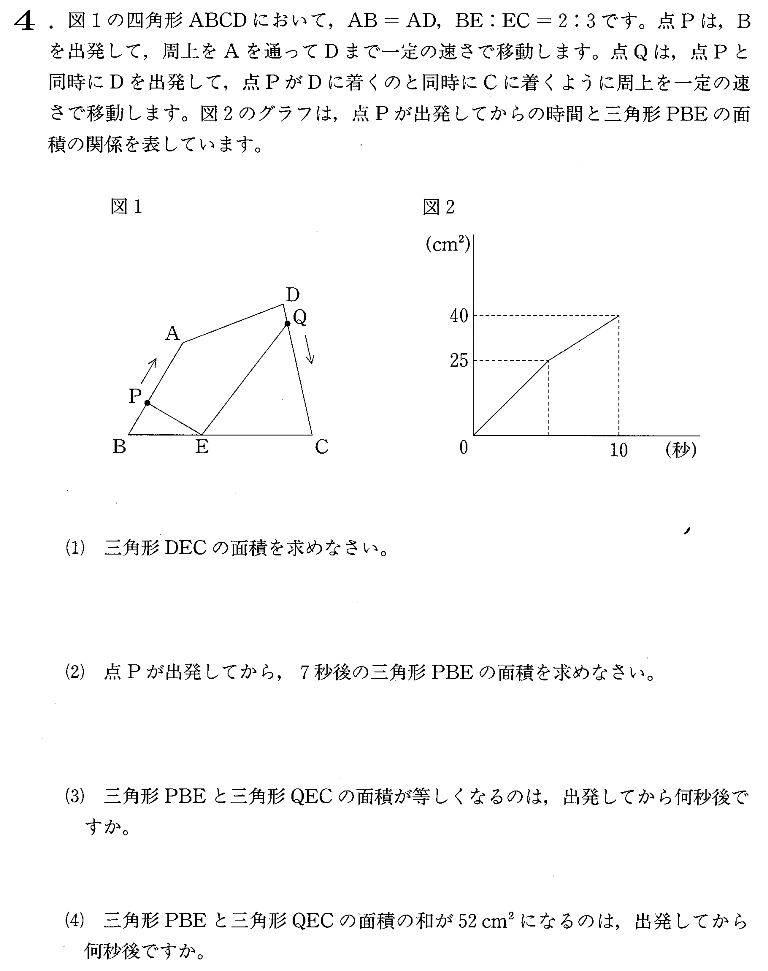
海城中学校2015年度1日目算数入試問題4.平面上の点移動 (1)解説解答
| (1) 三角形DECの面積を求めなさい。 |
| 解説 |
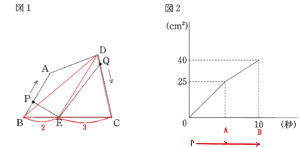 |
| 点Pが出発して10秒後Dに到着したときの三角形PBE = 三角形DBEの面積は図2より、40c㎡。 BE:EC = 2:3なので、三角形DBE:三角形DBE = 2:3 三角形DBEの面積は40c㎡なので、三角形DECの面積は40÷2×3 = 60。 |
| 答 60c㎡。 |
海城中学校2015年度1日目算数入試問題4.平面上の点移動 (2)解説解答
| (2) 点Pが出発してから、7秒後の三角形PBEの面積を求めなさい。 |
| 解説 |
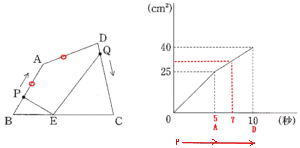 |
| AB = AD なので 点PがBを出発して5秒後にAを通過する。よって 7秒後は点PがAD上にあるとき。 点PはAD上を移動するとき5秒間に三角形PBEの面積は40 – 25 = 15c㎡増える。 1秒間に15÷5 = 3c㎡ずつ増えるので、2秒間では 3×2 = 6c㎡ したがって 25 + 6 = 31 |
| 答 31c㎡ |
海城中学校2015年度1日目算数入試問題4.平面上の点移動 (3)解説解答
| (3) 三角形PBEと三角形QECの面積が等しくなるのは、出発してから何秒後ですか。 |
| 解説 |
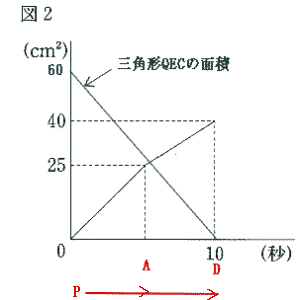 |
| 三角形QECは面積が60c㎡から10秒間でなくなるので、1秒間に60÷10 = 6c㎡ずつ減っていく。 PとQが同時にBとDを出発して5秒後の三角形PBEの面積は25c㎡,三角形QECの面積は 60 – 6×5 = 30c㎡ このときの三角形PBEの面積と三角形QECの面積の差は5c㎡. 三角形PBEは出発して5秒後からは1秒間に3c㎡ずつ増え、三角形QECは1秒間に6c㎡ずつ減っていく。 したがって 三角形PBEと三角形QECの面積が等しくなるのは同時に出発してから |
| 別解:相似比で解く |
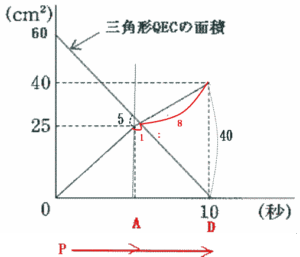 |
| 図の通り 5:40 = 1:8 三角形PBEと三角形QECの面積が等しくなるのは同時に出発してから |
海城中学校2015年度1日目算数入試問題4.平面上の点移動 (4)解説解答
| (4) 三角形PBEと三角形QECの面積の和が52c㎡になるのは、出発してから何秒後ですか。 |
| 解説 |
| 出発して5秒間は、三角形PBEの面積は1秒間に5c㎡ずつ増え、三角形QECの面積は6c㎡ずつ減っていく。よって和は60c㎡から1秒間に1c㎡ずつ減っていく。 |
| 出発して5秒後からは、三角形PBEの面積は1秒間に3c㎡ずつ増え、三角形QECの面積は6c㎡ずつ減っていく。よって和は25 + 30 = 55c㎡から1秒間に3c㎡ずつ減っていく。6秒後 55 – 3 = 52 |
| したがって三角形PBEと三角形QECの面積の和が52c㎡になるのは、出発して6秒後。 |
| 答 6秒後 |
