慶應義塾女子高等学校数学過去問研究
慶応義塾女子高等学校は 一般入試・帰国生入試とも同一問題です。
2016年度慶応義塾女子高等学校数学入試問題は1.独立小問2問 2.確率 3.平面図形 4.関数のグラフ 5.空間図形が出題され、例年通りの出題内容でした。また、例年通り証明問題はありませんでしたが、作図が出題されました。
今回は3.平面図形を解説します。
記事の作成者:プロ家庭教師集団スペースONEとは
慶応義塾女子高校2016年度数学入試問題3. 平面図形
慶応義塾女子高等学校は 一般入試・帰国生入試とも同一問題です。
2016年度慶応義塾女子高等学校数学入試問題は1.独立小問2問 2.確率 3.平面図形 4.関数のグラフ 5.空間図形が出題され、例年通りの出題内容でした。また、例年通り証明問題はありませんでしたが、作図が出題されました。
今回は3.平面図形を解説します。
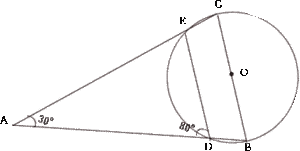
| [1] ∠ABCと∠EBCの大きさを求めなさい。 |
| ∠ABC 解説解答 |
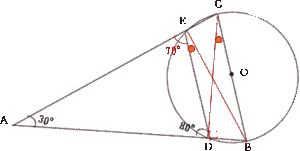 |
| BとE,CとDを直線で結ぶ。∠DEA = 180 – (80 + 30) = 70° ∠CEB = 90°(直径の円周角) なので、∠BED = 180 – (90 + 70) = 20° ∠BED = ∠BCD = 20°(弧DBの円周角) △DBCにおいて、∠CDB = 90°(直径の円周角),∠BCD = 20° したがって ∠DBC = ∠ABC = 180 – (90 + 20) = 70° |
| 答 70° |
| ∠EBC 解説解答 |
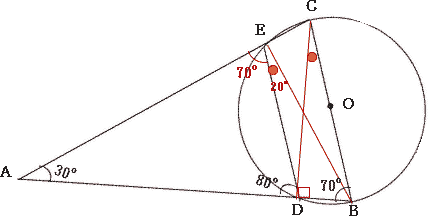 |
| ∠EBC = ∠ABC – ∠ABE ∠ABC = 70° ∠ABE = 180°- (∠EAB + ∠DEA + ∠BED) = 180°- (30°+ 70°+ 20°) = 60° したがって ∠EBC = 70°- 60°= 10° |
| 答 10° |
| [2] ∠DOEの大きさを求めなさい。 |
| 解説 |
| 円周角と中心角の性質より∠EBC = 2∠EOC = 10° なので、∠EOC = 20° ∠BCD = 2∠BOD = 20° なので、∠BOD = 40° ∠DOE = 180°- (∠EOC + ∠BOC) = 180°- (20°+ 40°) = 120° |
| 答 120° |
| [3] この円の半径をrとおくとき、線分DEの長さをrを用いて表しなさい。 |
| 解説 |
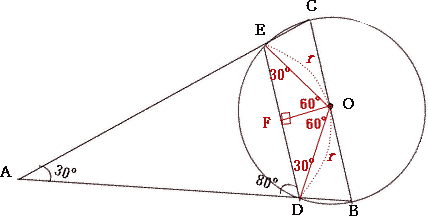 |
| 円の中心OからEDに垂線を引き、その交点をFとする。 ∠DOE = 120°なので、∠DOF = ∠EOF = 60°,OE = OD (半径),∠OEF = 180°- (∠EOF + ∠OFE) = 180°- ( 60°+ 90°)= 30° ∠ODF = 180°- (∠DOF + ∠OFD) = 180°- ( 60°+ 90°)= 30° したがって 90°,30°,60°の三角形の辺の比より 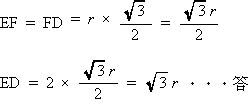 |
| [4] △ADEの面積をS,△ABCの面積をTとおくとき、S:Tを求めなさい。 |
| 解説 |
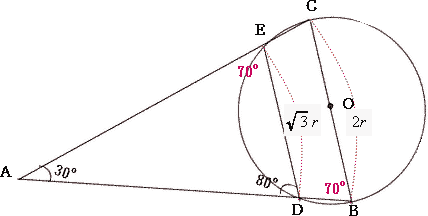 |
| △ADEと△ACBにおいて、 ∠EAD = ∠BAC = 30°, ∠DEA = ∠CBA = 70° 二角相等なので、△ADE ∽ △ACB ∠ODF = 180°- (∠DOF + ∠OFD) = 180°- ( 60°+ 90°)= 30° したがって 90°,30°,60°の三角形の辺の比より 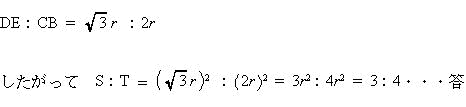 |
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00