芝中学・高等学校過去問研究
このグラフ問題は芝中学の定番です。解答に必要な目の付け所をしっかり身に着けましょう。
芝中の速さのグラフ問題は、ほかの中学の入試問題にはなかなか類題がありません。
芝中を志望する受験生は過去問を繰り返し練習して本番に備えましょう。
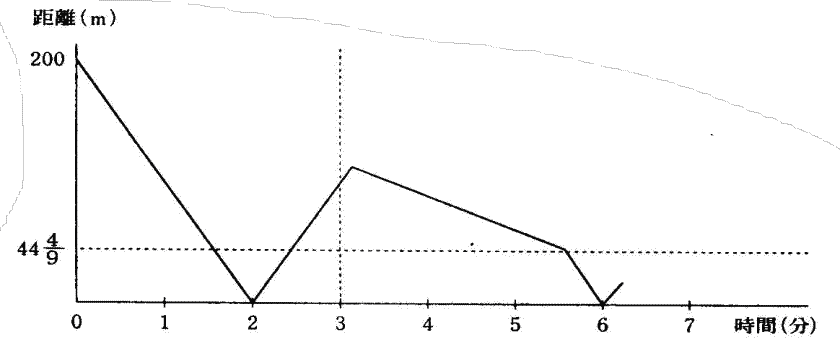
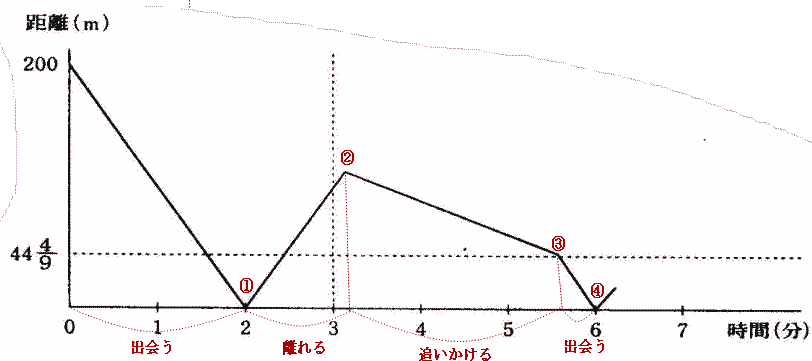
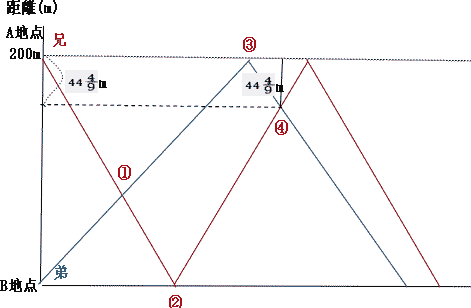
芝中学の定番グラフ問題は2点間の位置関係の理解がキーポイントです。
(2)は上位校によく出る速さの数列の問題です。上位校を志望する受験生もこのような問題は繰り返し練習してください。
(2)は上位校によく出る速さの数列の問題です。上位校を志望する受験生もこのような問題は繰り返し練習してください。
算数入試問題(速さのグラフにチャレンジ)