2007年度は男女難関校で速さの出会い・追いかけ算を出題していました。
麻布中学校の速さの問題は速さの出会いと追いかけ算の基本問題でした。解法は3種類で説明します。中学受験の特殊算の解法は1つではありません。中学受験では限られた時間で解かなければいけません。様々な解法で最短で正解にたどり着けるよう学習しましょう。
麻布中学校2007年度算数入試問題(速さの出会いと追いかけ算にチャレンジ)
麻布中学校2007年度算数入試問題 旅人算 問題
ある池の周りをA君とB君は同じ方向に、C君は逆方向に、それぞれ一定の速さで回ります。
A君はB君を15分ごとに追い越し、B君はC君と2分ごとに出会います。
B君が7分かかって走る距離をC君は8分で走ります。
このとき、A君とC君の速さの比を求めなさい。
麻布中学校2007年度 算数入試問題 旅人算 速さの出会いと追いかけ 解法1
A君はB君を15分ごとに追い越し・・・速さの追いかけ算(速さの差)
B君はC君と2分ごとに出会います・・・速さの出会い算(速さの和)
B君が7分かかって走る距離をC君は8分で走ります。・・・B君とC君の速さの比 8:7
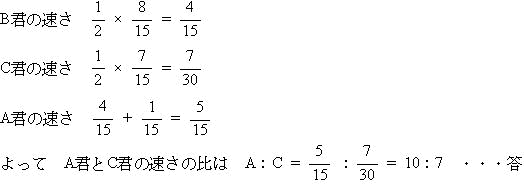
麻布中学校2007年度 算数入試問題 旅人算 速さの出会いと追いかけ 解法2
B君とC君の速さの比 8:7B君とC君は2分ごとに出会うので、池の周りの長さは 2×(8+7)=30
AはBを15分後とに追い越すのでAとBの速さの差は 30÷15=2
Aの速さは 8+2=10
答え 10:7
麻布中学校2007年度 算数入試問題 旅人算 速さの出会いと追いかけ 解法3
B君が7分かかって走る距離を、C君は8分で走ることから、B君とC君の速さの比は B:C=8:7

