開成学園　開成中学校過去問対策

2007年度は男女難関校で速さの出会い・追いかけ算を出題していました。

開成中学校の速さの問題では(1)，(2)は　基本レベル、(3)が条件整理を必要とする開成中ならではの煩雑問題でした。


開成中学校2007年度算数入試問題　4.速さの出会いと追いかけ算　問題

一定の速さで一つの円周をまわる３つの点A,B,Cがあります。AとBは同じ向きに、CはA,Bとは反対の向きに進みます。

３つの点A,B,Cが同じ地点から１時ちょうどに出発しました。

AとCは１時２分に、BとCは１時７分に、出発後初めて出会いました。

また、Aは１時２分３０秒に初めて元の地点に戻りました。

(1) Bが初めて元の地点に戻る時刻を求めなさい。

(2) AがBに初めて追いつく時刻を求めなさい。

(3) A,B,Cが初めて正三角形の３つの頂点となる時刻を求めなさい。

開成中学校2007年度算数入試問題　4.速さの出会いと追いかけ算　(1) 解説解答

(1) Bが初めて元の地点に戻る時刻を求めなさい。

３人の旅人算は共通の距離を見つけていくことから解法が始まる場合が多いです。

麻布の出会いと追いかけ算もそうでしたね。

開成の１番の問題も共通の道のりで歩く時間の差から始まります。

解説解答

AとCは１時２分に出発後初めて出会い、Aは1時2分30秒に初めて元の地点に戻ったので、

AがCに出会うまでにかかった時間は2分間。その後元の位置に戻るまでにかかった時間は30秒。

円周を直線にして考えましょう。



Cが2分かかった距離を、Aが30秒で進んだことになる。

AとCの　時間の比は　30：2×60 = 1：4

よって　速さの比は　A：C = 4：1

円周の長さは速さ4のAと速さ1のCが２分間で出会う距離になるので

(4 + 1) ×2 = 10

BとCは１時７分に、出発後初めて出会ったので

Cが速さ1で7分間に進む距離は　1×7 = 7

Bは 7分間で　10 – 7 = 3進んでいるので、10の道のりを進むのにかかる時間は



答　　1時　23分　20秒

別解

答　　1時　23分　20秒　　　

開成中学校2007年度算数入試問題　4.速さの出会いと追いかけ算　(2) 解説解答

基本レベルの追いかけ算です。さっさと答えてしまいましょう。

(2) AがBに初めて追いつく時刻を求めなさい。

解説



AがBに追いつく時刻は１周10だけAがBより多く進めばいいので、当然追いかけ算は速さの差で計算できますね。


答　1時2分48秒


別解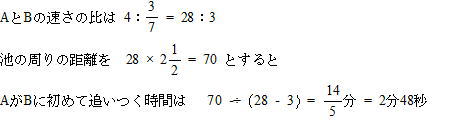



答　1時2分48秒

開成中学校2007年度算数入試問題　4.速さの出会いと追いかけ算　(3)　解説解答

(3)　A,B,Cが初めて正三角形の３つの頂点となる時刻を求めなさい。
解説

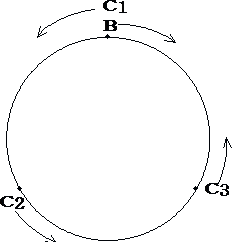C1はBと出会うときであるから 0分　7分　14分　21分　…

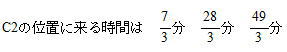次にBとAの相対的位置関係を調べてみます。

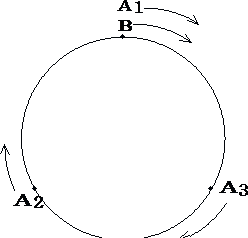ここでC2とA3が同じ時間になるときか、C3とA2が同じ時間になる時を調べます。

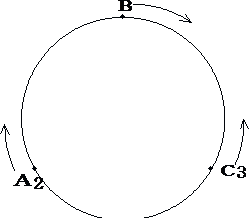
答　１時４分４０秒
　　　　　

開成中学校2007年度算数入試問題　4.速さの出会いと追いかけ算　(3)　別解

A,B,Cが初めて正三角形の３つの頂点となる時刻を求めなさい。

解説

三角形ABCが正方形になるとき　　　

辺AB = 辺BC = 辺CA　　よってAB間の距離 = BC間の距離 = CA間の距離　　

この場合下図のように2通り考えられます。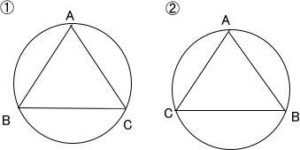




まず①の場合から考えていきます。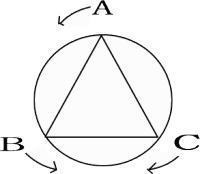




2回目はこのときからさらに1周分進んだときなので、10÷（4 + 1）= 2・・・2分後　　

2分40秒 ， 2分40秒 + 2分 = 4分40秒，2分40秒 + 2分×2 = 6分40秒，・・・・・

　　

4分40秒，4分40秒 + 7分 = 11分40秒，4分40秒 + 7×2，・・・

②の場合
　　

　1分20秒，1分20秒 + 2分，1分20秒＋2分×2，・・・・・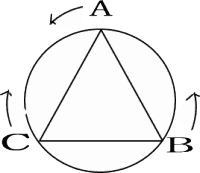

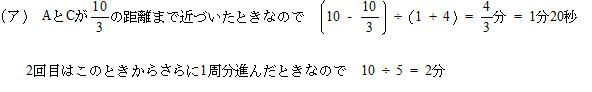
①②よりA，B，Cが初めて正三角形の3つの頂点になるのは　出発して　4分40秒後　　

答　1時4分40秒