青山学院高等部過去問研究
青山学院高等部一般入試数学出題内容は 例年小問5問、枝問各2～3の大問4問 9題構成です。確率・円周角が頻出問題です。
今回は2010年度一般数学入試問題４.平面図形の辺の比を解説します。解法は3通りです。
途中式を必要としない解答のみを解答欄に記入する解答形式なので、受験生にとって最も得意な解法でチャレンジしてください。
3のメネラウスの定理用いた解法は、高校数学の内容ですが、私立の中高一貫校では中学2・3年生で学習する場合も多いので、解説しました。
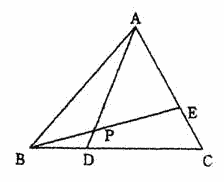
青山学院高等部2010年度 数学入試問題 4. 平面図形 問題
青山学院高等部2014年度数学入試問題4.平面図形 解法1
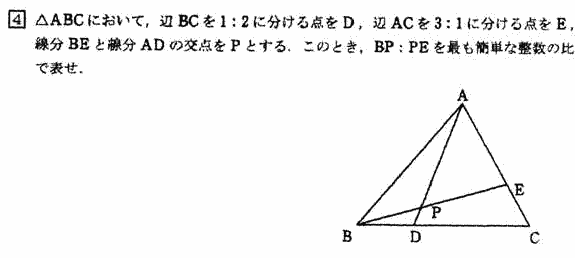
点Eを通りADと平行な直線を引き、BCとの交点をFとおく。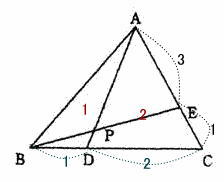 DF：FC = 3：1なので CF：FD = 3：1 よって BD：DF = 1：2×3/4 = 2：3 BD：DF = BP：PE なので BP：PE = 2：3 |
| 答 ２：３ |
青山学院高等部2014年度数学入試問題4.平面図形 解法2
点Pと点Cを直線で結ぶ。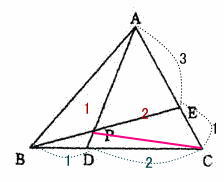 △ABP：△APC = 1：2 △CPE：△APE = 1：3 なので △ABP：△APE = 1：2×3/4 = 2：3 よって BP：PE = 2：3 |
| 答 ２：３ |
青山学院高等部2014年度数学入試問題4.平面図形 解法3 メネラウスの定理
| メネラウスの定理 |
図のように△ABＣの辺ＢＣ，ＣＡ，ＡＢまたはその延長が１つの直線とそれぞれ点Ｐ，Ｑ，Ｒでまじわるとき、 |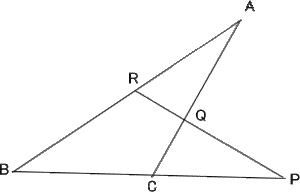
 が成り立つ。 |
| メネラウスの定理より |
 |
 |
 |
 |
| よって BP：PE＝２：３ |
| 答 ２：３ |