秋田県立高等学校数学過去問研究
今回は 2010年度秋田県立高校数学入試問題5の平面図形問題を解説します。5はⅠ,Ⅱ,Ⅲの中から指示された問題を答えます。それぞれ段階的に難易度が高くなっています。
Ⅰは基本レベルの問題です。相似形と三平方の定理の基本の復習をしましょう。
記事の作成者:プロ家庭教師集団スペースONEとは
秋田県立高校2010年度数学入試問題5-1. 平面図形の折り返し
今回は 2010年度秋田県立高校数学入試問題5の平面図形問題を解説します。5はⅠ,Ⅱ,Ⅲの中から指示された問題を答えます。それぞれ段階的に難易度が高くなっています。
Ⅰは基本レベルの問題です。相似形と三平方の定理の基本の復習をしましょう。
| ∠ BAC = 30°,∠ACB = 90°,BC = 6cmの直角三角形ABCについて,次の(1),(2)の問いに答えなさい。 |
| (1) 図1のように,点A が点C にくるように折り返し,折り目を線分DE とする。 ① ∠ EDC の大きさを求めなさい。 ② △ ABC の面積は,△ DCE の面積の何倍か求めなさい。 |
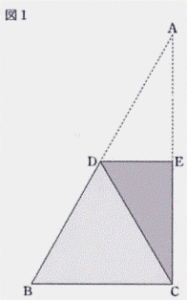 |
| (2) 図2のように,点A が点B にくるように折り返し,折り目を線分FG とする。線分BG の長さを求めなさい。 |
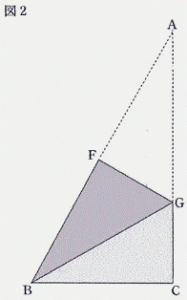 |
| (1) 図1のように,点A が点C にくるように折り返し,折り目を線分DE とする。 |
| ① ∠ EDC の大きさを求めなさい。 |
| 解説 |
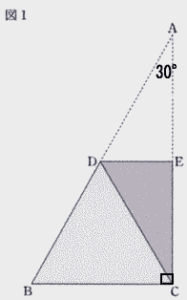 |
| 三角形ABCの内角の和は 180° ∠ACB = 90° ∠BAC = 30° よって ∠EDC = 90 ー 30 = 60 |
| 答 60° |
| ② △ ABC の面積は,△ DCE の面積の何倍か求めなさい。 |
| 解説 |
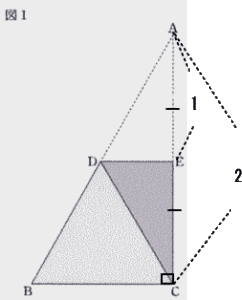 |
| 点A が点C にくるように折り返しているので、AE = EC |
| ⊿DCE ≡ ⊿DAE, ⊿ADE ∽ ⊿ABC より |
| AE:AC=1:2 |
| ⊿DCEと⊿ABCの面積比は 1×1:2×2=1:4 |
| 答 4倍 |
| (2) 図2のように,点A が点B にくるように折り返し,折り目を線分FG とする。線分BG の長さを求めなさい。 | |
 | |
| 解説 | |
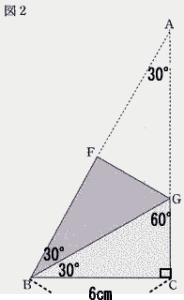 | |
| ⊿BGCにおいて ∠BAC = ∠FBG = 30°, ∠ACB = 90°なので ∠BGC = 60° | |
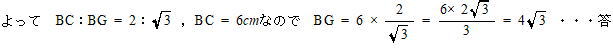 |
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00