フェリス女学院中学校・高等学校算数過去問研究
フェリス女学院中学校の2014年度算数入試問題は例年通り計算1問を含む小問集合,大問構成でした。
大問は、2.平面図形(円の性質) 3.平面図形と平面上の点移動 4.立体図形上の点の場合の数 5.整数の性質の出題でした。
例年通りの出題構成で今後も平面図形・立体図形を中心とした出題傾向は続くと考えられます。
フェリス女子学院中学校2014年度の志望者数396名,受験者数385名,合格者192名,算数合格者平均点は53点(昨年度比+6点)でした。
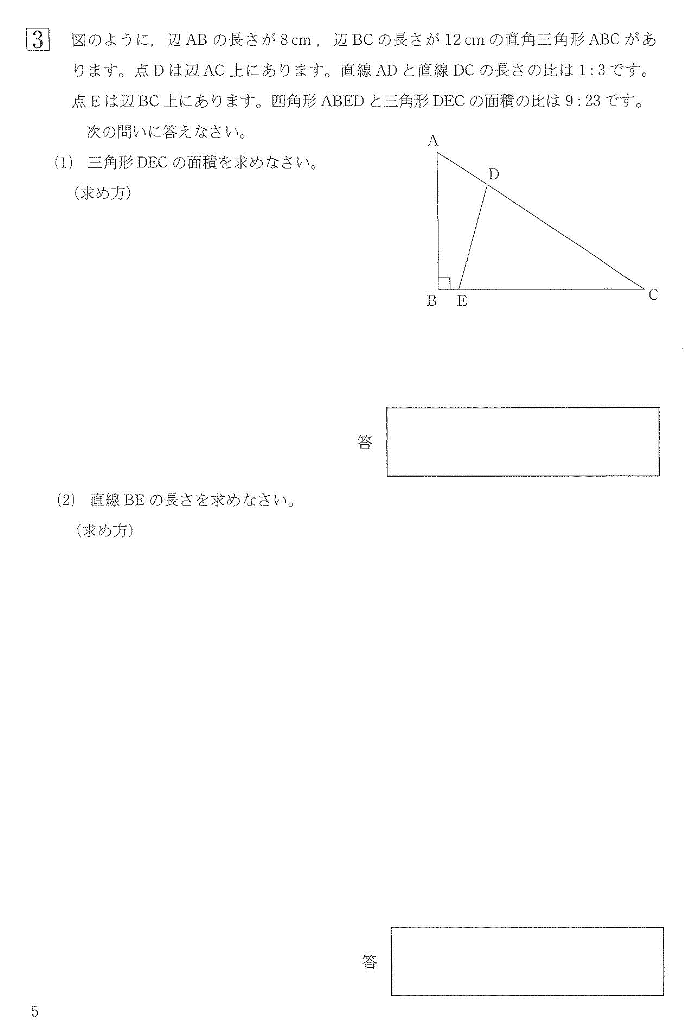
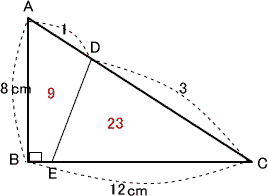
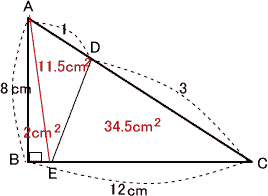
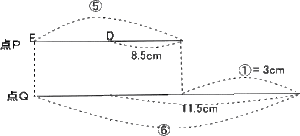
今回は (3)平面図形と平面上の点移動を解説します。
例年通りの出題構成で今後も平面図形・立体図形を中心とした出題傾向は続くと考えられます。
フェリス女子学院中学校2014年度の志望者数396名,受験者数385名,合格者192名,算数合格者平均点は53点(昨年度比+6点)でした。
今回は (3)平面図形と平面上の点移動を解説します。
算数入試問題(平面図形と平面上の点移動にチャレンジ)