フェリス女学院中学校・高等学校算数過去問研究
フェリス女学院中学校の2015年度算数入試問題解説解答は4.平面図形を解説します。
辺の長さや高さが解らない場合、どういう解き方があるかを考える良問です。
(1) は(2)(3)のヒントになっています。
辺の長さや高さが解らない場合、どういう解き方があるかを考える良問です。
(1) は(2)(3)のヒントになっています。
算数入試問題（平面図形にチャレンジ）
フェリス女学院中学校2015年度 算数入試問題 2.平面図形 問題
| 図のように、1辺が12cmの正方形ＡＢＣＤと直角三角形ＥＦＧがあります。 |
 |
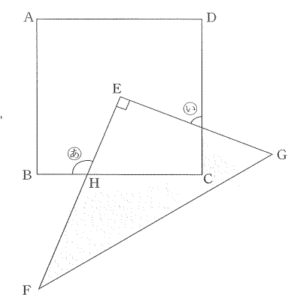辺ＥＦの長さは16cm，辺ＦＧの長さは20cm，辺ＧＥの長さは12cmです。 点Ｅあ、正方形ＡＢＣＤの2ほんの対角線が交わってできる点です。 辺ＢＣと辺ＥＦに交わる点をＨとします。 次の問いに答えなさい。 (1) (あ)の角度が115°のとき、(い)の角度を求めなさい。 (2) 図の斜線部分の面積を求めなさい。 |
フェリス女学院中学校2015年度 算数入試問題 2.平面図形 (1) 解説解答
| (1) (あ)の角度が115°のとき、(い)の角度を求めなさい。 |
| 解説 |
| 辺ＣＤと辺ＥＧとの交点をＩとする。 |
 |
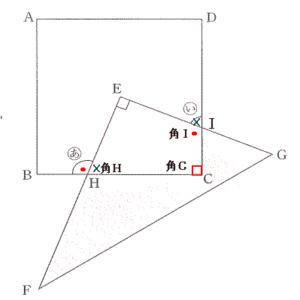四角形ＥＨＣＩの内角の和は360° 角Ｃと角Ｅはそれぞれ90°なので、角Ｈ＋角Ｉ = 180° (あ)＋角Ｈ = 180°，角Ｉ + (い) = 180° よって (あ) = 角Ｉ したがって (い) = 180°- (あ) = 180° – 115° = 65° |
| 答 65° |
フェリス女学院中学校2015年度 算数入試問題 2.平面図形 (2) 解説解答
| (2) 図の斜線部分の面積を求めなさい。 |
| 解説 |
 |
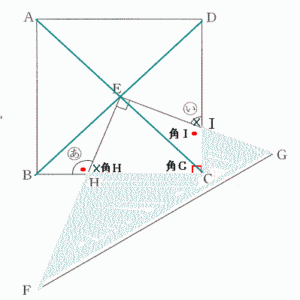| 角ＥＣＩと角EBHは直角を対角線で２等分しているので45度 (1)より 角CＩE = 角(あ) 直線ＢＥと直線ＣＥは対角線を二等分した長さ。 よって 三角形ＥＣＩと三角形ＥＢＨは合同な三角形なので、 斜線部分の面積は 直角三角形ＥＦＧの面積から正方形ＡＢＣＤの面積の1/4を引いて求められる。 16×12÷2 – 12×12÷4 = 60 |
| 答 ６０ｃ㎡ |
フェリス女学院中学校2015年度 算数入試問題 2.平面図形 (3) 解説解答
| (3) 直線ＦＨの長さが9cmのとき、斜線部分の周りの長さを求めなさい。 |
| 解説 |
 |
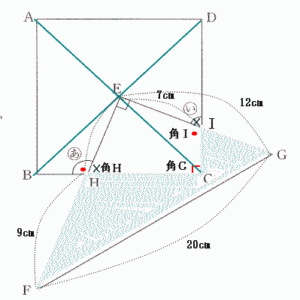| 三角形ＥＣＩと三角形ＥＢＨは合同な三角形なので、 EI = EH FH = 9cm なので EH = EI = 16 – 9 = 7cm よって IC = 12 – 7 = 5cm また BH = IC なので BH + HC = IC + HC = 12cm 以上から 斜線部分の周りの長さ IC + GF + IH + HC + CI = 5 + 20 + 9 + 12 = 46 |
| 答 46cm |