桐朋中学校過去問研究
桐朋中学校2008年度 算数入試問題 7.平面上の点移動 問題
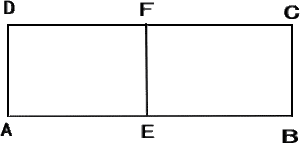
| 図のように、辺AB,ADの長さがそれぞれ24cm、6cmの長方形ABCDがあります。 EFはそれぞれ辺AB,CDを2等分する点です。点Pは点Aを出発し、毎秒2cmの速さで長方形ABCDの辺上をA,B,C,D,A,B,・・・の順にまわります。 点Qは点Pと同時に点Aを出発し、毎秒3cmの速さで長方形ADFEの辺上をA,D,F,E,A,D・・・の順に回ります。 点P,Qは、点Aを出発してから初めて同時に点Aに着いたとき、そこで止まります。 |
 |
| (1) 点P,Qが点Aを出発してから止まるまでにかかる時間は何秒ですか。 |
| (2) 3つの点A,P,Qを結んでできる三角形APQの面積が長方形ABCDの半分になるのは、点P,Qが点Aを出発してから何秒後と何秒後ですか。 |
| (3) 4つの点A,E,P,Qを結んでできる四角形AEPQが平行四辺形になるのは、点P,Qが点Aを出発してから何秒後ですか。考えられるものをすべて書きなさい。 |
桐朋中学校2008年度 算数入試問題 7.平面上の点移動 (1) 解説解答
(1) 点P,Qが点Aを出発してから止まるまでにかかる時間は何秒ですか。
解説
Pは1周60cmを毎秒2cmでまわるので、1周するのにかかる時間 60÷2=30秒
Qは1周30cmを毎秒3cmでまわるので、1周するのにかかる時間 36÷3=12秒
点P,Qが、点Aを出発してから初めて同時に点Aに着く時間 30と12の最小公倍数 答 60秒
桐朋中学校2008年度 算数入試問題 7.平面上の点移動 (2) 解説解答
解説
Pが頂点にくるとき:B,C,D,Aの順に,12,15,27,30,42,45,57,60秒後,
Qが頂点にくるとき:D,F,E,Aの順に,2,6,8,12,14,18,20,24,26,30,32,36,38,42,44,48,50,54,56,60秒後。
点Qが点Dにいて,点PがBC上にくるのは14秒後,
点Qが点Fにいて,点Pが点Bにくるのは42秒後。
答 14秒後, 42秒後
桐朋中学校2008年度 算数入試問題 7.平面上の点移動 (3) 解説解答
(3) 4つの点A,E,P,Qを結んでできる四角形AEPQが平行四辺形になるのは、点P,Qが点Aを出発してから何秒後ですか。考えられるものをすべて書きなさい。
解説点P,QともにCD上にあるとき:
15秒後・・・DQ 3×(15-14)=3(㎝),CP+DQ=24-12=12(㎝),15+(12-3)÷(2+3)=16.8(秒後)
50秒後・・・CP 2×(50-45)=10(㎝),50+(12-10)÷(2+3)=50.4(秒後)
点PがBC上,点QがEF上にあるとき:
42秒後から 42+6÷(2+3)=43.2(秒後)
答 16.8秒後, 50.4秒後, 43.2秒後
