東京都市大学等々力中学校帰国生過去問対策

2021年度の東京都市大学等々力中学校帰国生入試は募集人数20名，出願資格は① 現在国内に在住し海外在住1年以上で原則帰国後3年以内　② 現在海外に在住し令和3年4月1日までの海外在住機関が1年以上の者　です。
受験教科は算数・作文必修，英語・国語選択　面接は個人グループです。

2020年度算数入試問題は　1.四則計算3問　2.小問集合5問　3.平面図形　4.割合　5.流水算　6.場合の数でした。

今回は算数入試問題3.平面図形を解説します。相似比と面積比に注意して解きましょう。

東京都市大学等々力中学校2020年度　帰国生算数入試問題　3.平面図形　問題

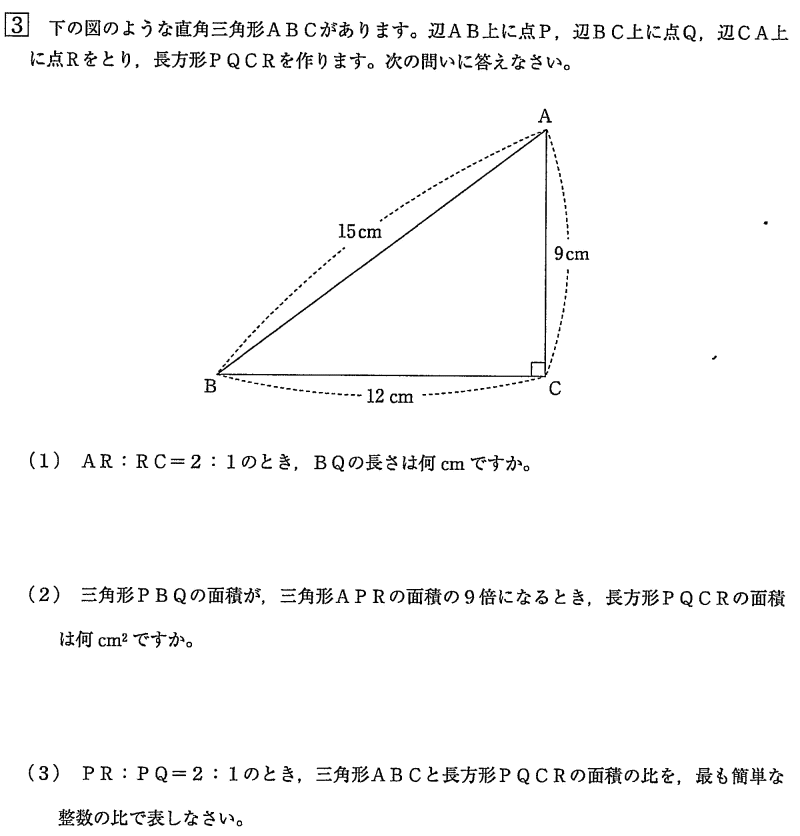
東京都市大学等々力中学校2020年度　帰国生算数入試問題　3.平面図形　(1)解説解答

(1)　AR：RC = 2：1のとき、BQの長さは何cmですか。

解説解答

四角形PQCRは長方形なので、向かい合う辺の長さは等しく、かつ一つの内角の大きさは全て90°。

よって　下図の通り。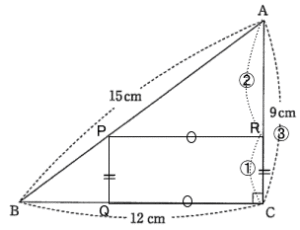



三角形APRと三角形ABCは相似形なので、AR：AC = PR：BC = 2：3

BC = 12cmなので



PR = QC = 8cmなので

BQ = 12 – 8 = 4

答　　　　4cm

東京都市大学等々力中学校2020年度　帰国生算数入試問題　3.平面図形 (2)　解説解答

(2)　三角形PBQの面積が、三角形APRの面積の9倍になるとき、長方形PQCRの面積は何c㎡ですか。

解説解答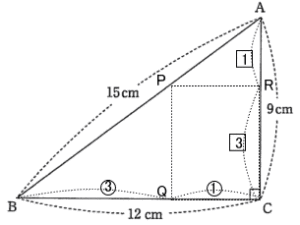



三角形PBQと三角形APRは相似形

三角形PBQと三角形APRの面積比が　9：1 = 3×3：1×1 なので　BQ：PR = 3：1

長方形の性質より　PR = QC 　よって　BQ：QC = 3：1

QC = 12cmなので



同様に　AR：RC = 1：3

AC = 9cmなので



①，②より長方形PQCRの面積は



別解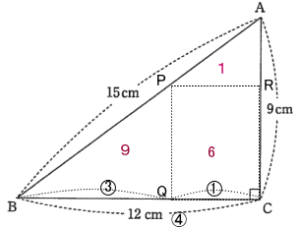



三角形PBQと三角形APRは相似形

三角形PBQと三角形APRの面積比が　9：1 = 3×3：1×1 なので　BQ：PR = 3：1

長方形の性質より　PR = QC 　よって　BQ：QC = 3：1　なので　BQ：BC = 3：4

したがって　三角形PQQの面積：三角形ABCの面積 = 3×3：4×4 = 9：16

また　三角形APBQの面積：三角形PBQの面積 = 9：1 なので、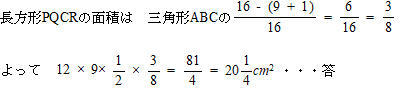

東京都市大学等々力中学校2020年度　帰国生算数入試問題　3.平面図形

(3)　PR：PQ = 2：1のとき、三角形ABCと長方形PQCRの面積の比を、最も簡単な整数の比で表しなさい。

解説解答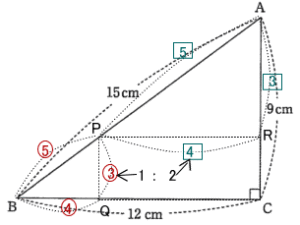



三角形ABCと三角形PBQと三角形APRは相似形。　

よって辺の比はAB：BC：CA = PB：BQ：QP = AP：PR：RA = 15：12：9 = 5：4：3

また　PR：PQ = 2：1なので

PQ = 3 のとき　PR = 6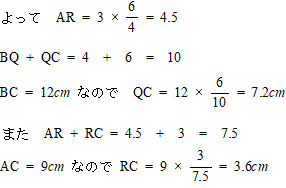



したがって　三角形ABCと長方形PQCRの面積の比は

12 ×9 ÷2 ： 7.2 × 3.6 = 6 ×9 ×100：72 ×36 = 25：12

答　　25：12