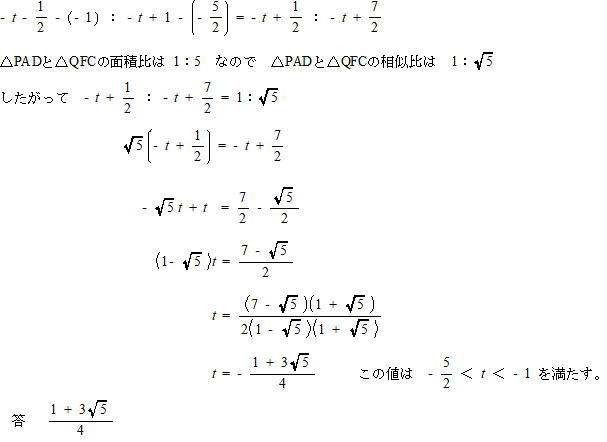開成高等学校数学過去問研究

開成高等学校2021年度数学入試問題は出題構成は例年通り大問4題ですが、出題内容は1の小問が無くなり、1.関数のグラフ　2.数の性質　3.場合の数　4.立体図形が出題されました。平面図形の証明問題の出題はされませんでしたが、理由を説明する出題はありました。全体として昨年度より難化しました。

今回は、1.関数のグラフを解説します。

開成高校2021年度数学入試問題2．関数のグラフ　問題

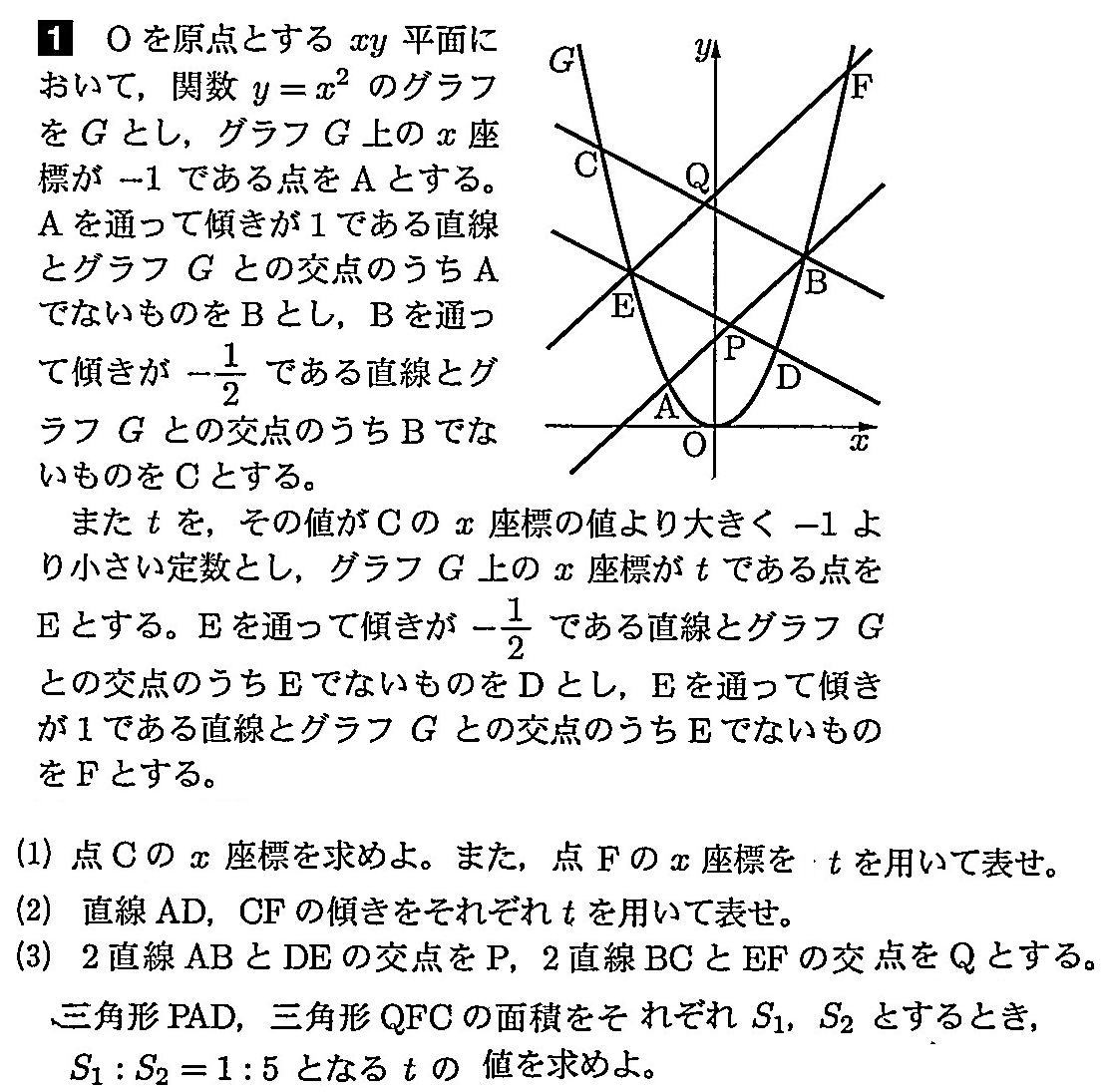
開成高校2021年度数学入試問題2．関数のグラフ (1) 解説解答

(1)　点Cのx座標を求めよ。また、点Fのx座標をtを用いて表せ。

点Cのx座標　解説解答

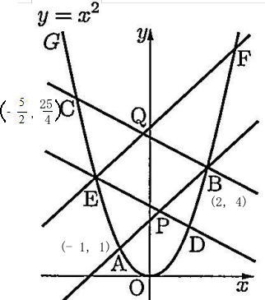
点Fのx座標　解説解答

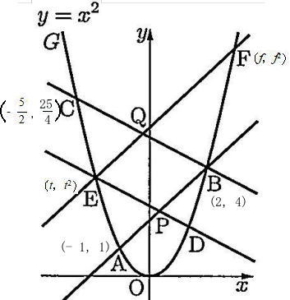
開成高校2021年度数学入試問題2．関数のグラフ (2) 解説解答

(2) 　直線AD，直線CFの傾きをそれぞれtを用いて表せ。

直線ADの傾き　解説解答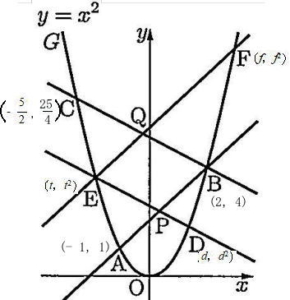







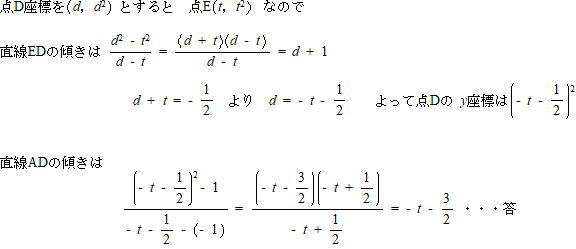
直線CFの傾き　解説解答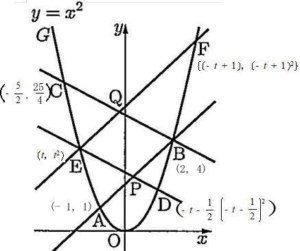

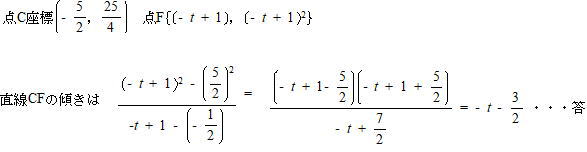
開成高校2021年度数学入試問題2．関数のグラフ (3) 解説解答

(3)　2直線ABとDEの交点をP，2直線BCとEFの交点をQとする。三角形PAD，三角形QFCの面積をそれぞれS1，S2とするとき、S1：S2 = 1：5 となるtの値を求めよ。

解説解答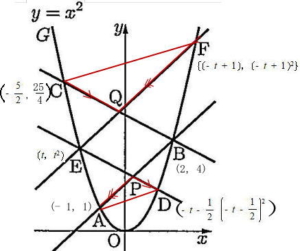



△PADと△QFCにおいて　PA // QF，DP //CQ　よって　AD // FC より　平行線の錯角は等しいので　∠PAD = ∠QFC，∠ADP = ∠FCQ

二角相等より　△PAD ∽ △QFC

相似比は　点Dと点Aのx座標の差 ： 点Fと点Cのx座標の差　より