2009年度の聖光学院中学校・高等学校の算数入試問題は、例年より1問増えて大問5題構成でした。1.仕事算 2.場合の数 3.合計と平均 4.平面図形 5.速さ の出題でした。
今回は 4.平面図形を解説します。 図1.は サピックスや啓明舎の演習問題にも取り上げられている東大寺学園中学の「伝説の名問題」を、聖光学院ならではの応用・難問にバージョンアップしての出題でした。
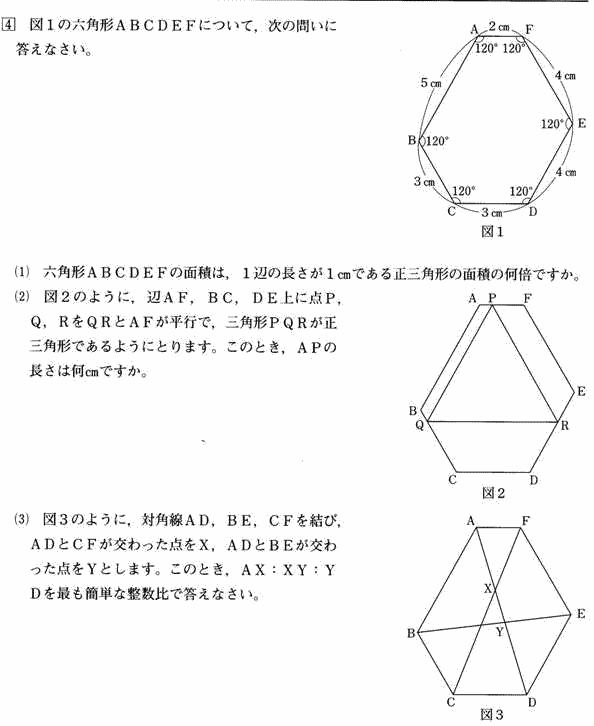
聖光学院中学校 2009年度 算数入試問題 平面図形 問題
聖光学院中学校 2009年度算数入試問題 解説解答
| (1) 六角形ABCDEFの面積は、1辺の長さが1cmである正三角形の面積の何倍ですか。 |
| 解説解答 |
| 正三角形の相似の問題です。相似形では面積の比は辺の比の二乗の比になります。 たとえば下の図形の面積比は A:B=1:9になります。 |
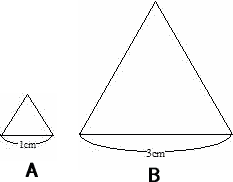 |
| 問題の図形は下図のように補助線を引きます。 |
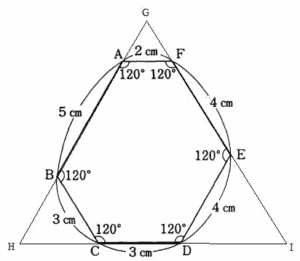 |
| すると一辺10cmの大きい正三角形が出来ます。 三頂点にある小さな正三角形の面積を引けば求める図形の面積になりますね。 一辺1cmの三角形の面積を1とおくとそれぞれの三角形の面積は △GHI=100 △GAF=4 △BHC=9 △EDI=16 六角形ABCDEFの面積は100-4-9-16=71 答 71倍 |
 |
| 解説解答 |
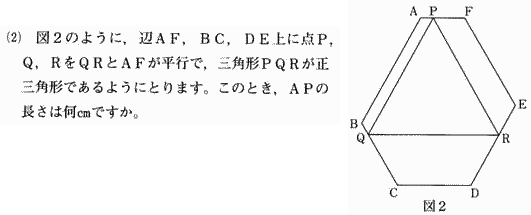
| この問題も六角形のままで考えてはいけません。これは下の図のように延長して大きな正三角形を作ります。 |
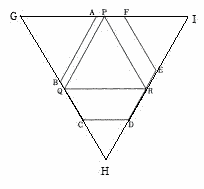 |
| 大きい正三角形の一辺は11cmになります。 正三角形のなかに三辺上の点を結んで正三角形を作るには、各辺の中点をつなぐ場合しかありません。 ですから GP=PIです。 GP=5.5cm GA=5cmより AP=0.5cm 答 0.5cm |
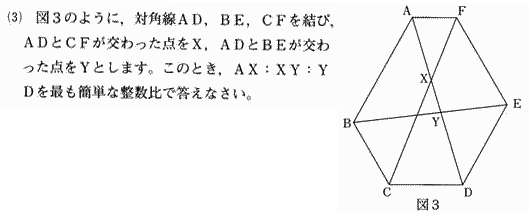 |
| 解説解答 |
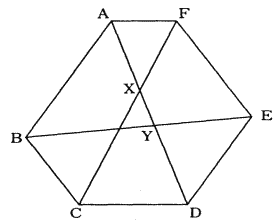 |
この問題を解く前に気づいてほしいことがあります。
プロ家庭教師集団スペースONEプロ家庭教師の聖光学院中学帰国入試過去問解説解答を頒布中です。メールでお問い合わせください。 |
