令和3年度第1回高等学校卒業程度認定試験問題解説解答
高等学校卒業程度認定試験は、様々な理由で、高等学校を卒業できなかった方等の学習成果を適切に評価し、高等学校を卒業した者と同等以上の学力があるかどうかを認定するための試験です。合格者は大学・短大・専門学校の受験資格が与えられます。また、高等学校卒業者と同等以上の学力がある者として認定され、就職、資格試験等に活用することができます。
(大学入学資格検定(大検)は、平成17年度より高等学校卒業程度認定試験にかわりました。)
受験資格は 16歳になる年度から受験できる。但し、既に大学入学資格を有している場合は受験できない。
※ 従前の大学入学資格検定では認められていなかった全日制高等学校等の在籍者にも、受験資格を付与している。
※ 合格科目は、学校長の判断により卒業単位として単位認定することができる。
実施回数・時期は 毎年2回(8月・11月)
試験科目・合格要件
| 教科 | 科目 | 合格要件 |
| 国語 | 国語 | |
| 地理歴史 | 世界史(A、B) | いずれか1科目 |
| 日本史(A、B)、地理(A、B) | いずれか1科目 | |
| 公民 | 現代社会 | いずれか一方 |
| 倫理と政治・経済 | ||
| 数 学 | 数 学 | |
| 理 科 | 科学と人間生活、物理基礎、化学基礎、 生物基礎、地学基礎 | 科学と人間生活を含む2科目 又は 科学と人間生活以外の3科目 |
| 外 国 語 | 英語 |
※ 合格に必要な科目数は、受験者の選択により8~10科目となる。
※ 合格者が18歳未満の場合は、満18歳の誕生日から合格者となる。
※ 合格科目は、学校長の判断により卒業単位として単位認定することができる。
高等学校卒業程度認定試験の入試問題は文部科学省ホームページで公開しています。
今回は 令和3年度英語問題か6.長文総合を解説します。
高等学校卒業程度認定試験令和3年度数学問題5.三角関数 問題
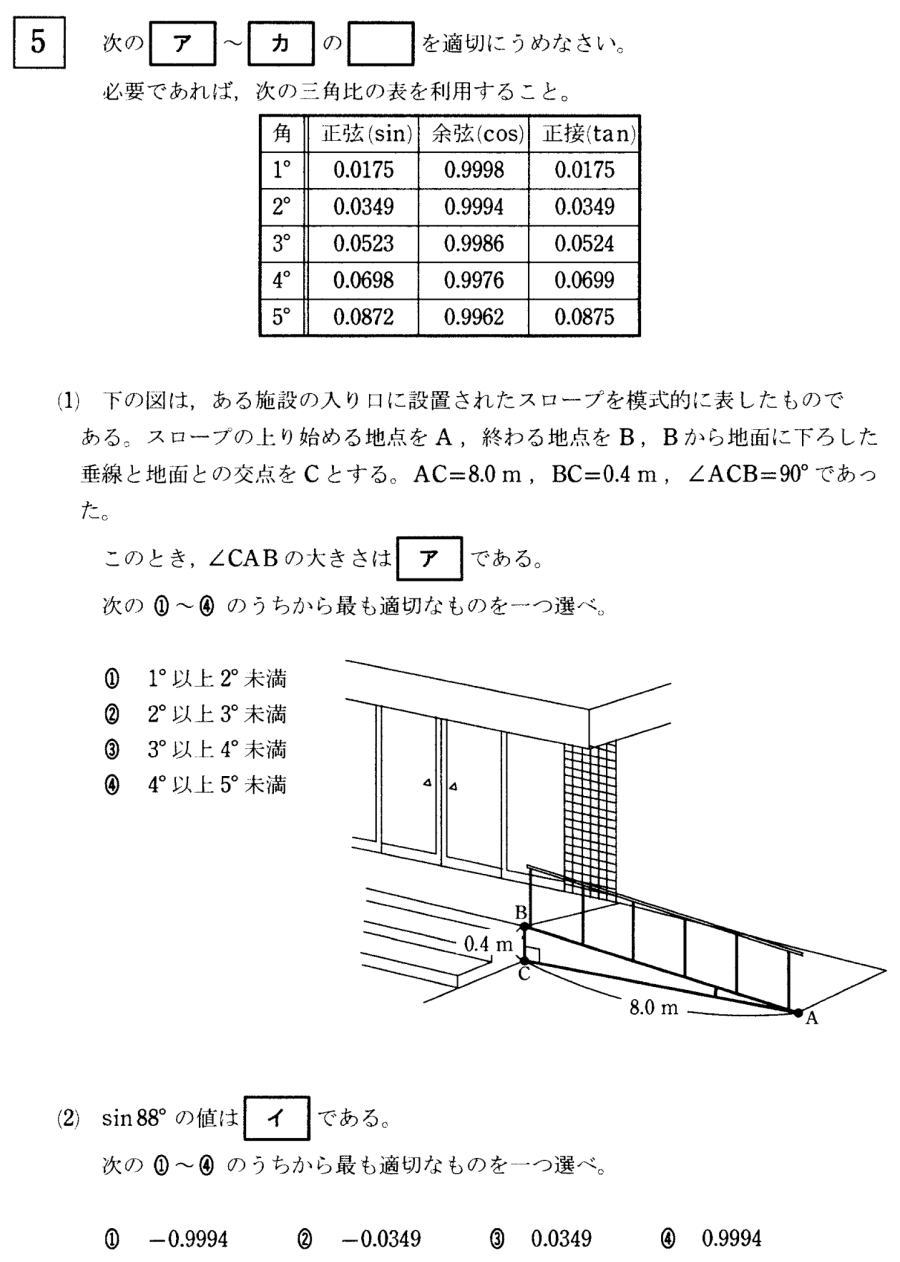
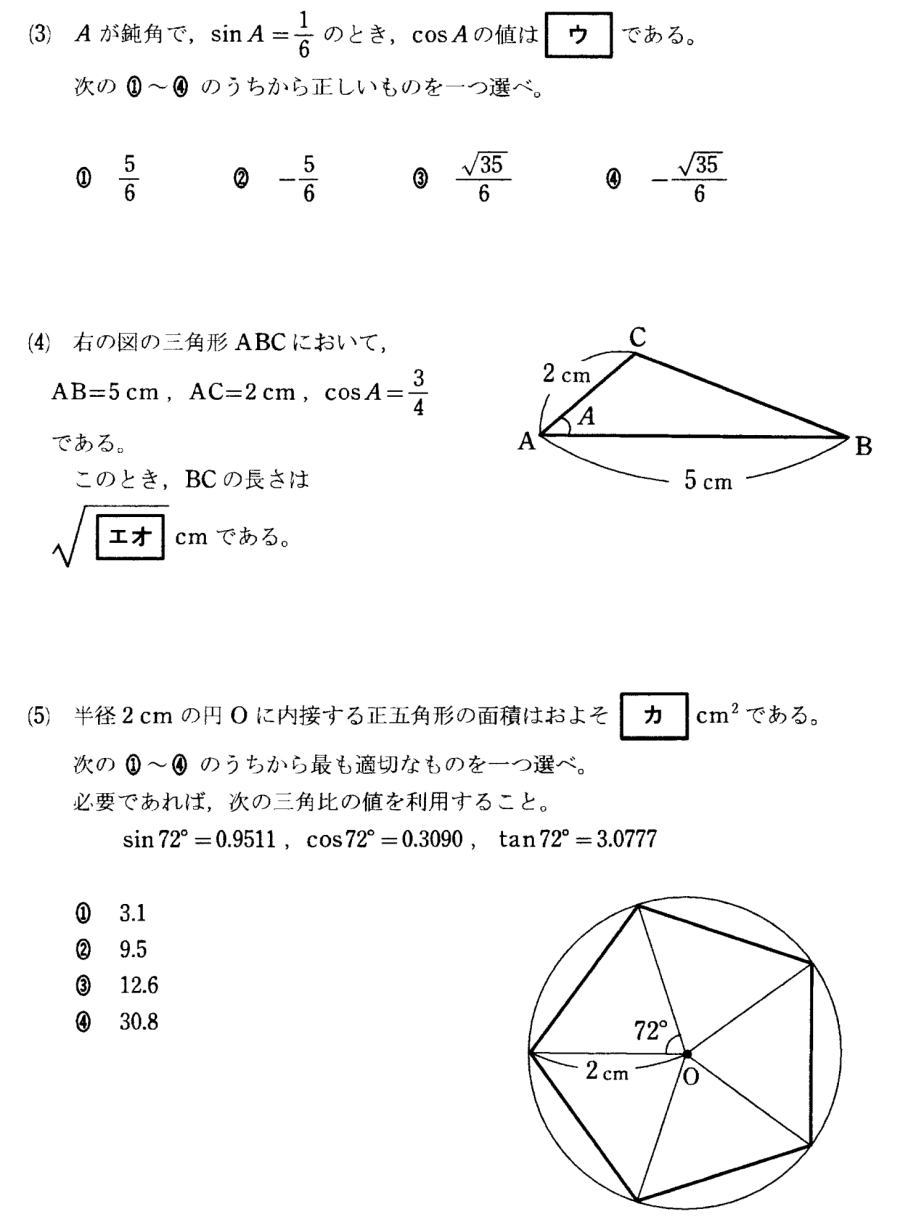
高等学校卒業程度認定試験令和3年度数学問題5.三角関数(1)解説解答
(1) 下の図は、ある施設の入り口に設置されたスロープを模式的に表したものである。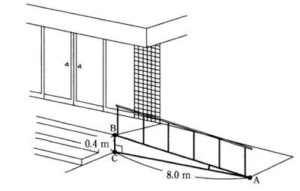
スロープのの折り始める地点をA, 終わる地点をB,Bから地面に下した垂線と地面との交点をCとする。AC = 8.0m,BC = 0.4m,∠ACB = 90°であった。このとき、∠CABの大きさは[ア]である。次の①~④のうちから最も適切なものを一つ選べ。
① 1°以上2°未満 ② 2°以上3°未満 ③ 3°以上4°未満 ④ 4°以上5°未満
解説解答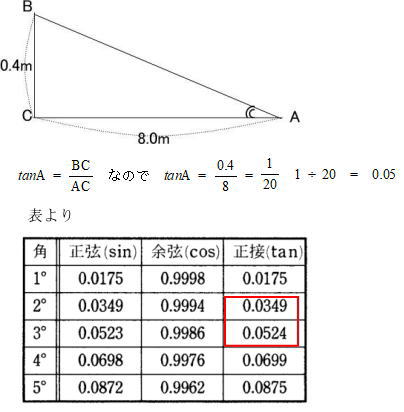
② 2°以上3°未満
答え ②
高等学校卒業程度認定試験令和3年度数学問題5.三角関数(2)解説解答
(2) sin88°の値は[イ]である。次の①~④のうちから最も適切なものを一つ選べ。
① -0.9994 ② -0.0349 ③ 0.0349 ④ 0.9994
解説解答
正弦(sin)の加法定理
sin(α + β) = sinαcosβ + cosαsinβ
sin(α – β) = sinαcosβ – cosαsinβ
sin88° = sin(90° – 2°)
= sin90°cos2° – cos90°sin2°
sin90° = 1.cos90° = 0なので
sin90°cos2° – cos90°sin2° = cos2°
表より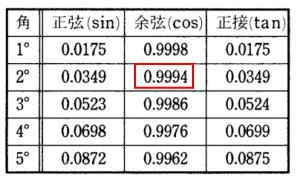
④ 0.9994
答え ④
高等学校卒業程度認定試験令和3年度数学問題5.三角関数(3)解説解答

答え ③
高等学校卒業程度認定試験令和3年度数学問題5.三角関数(4)解説解答

解説解答
余弦定理(三角形の辺の長さと内角の予言の間に成り立つ関係を示した定理)
△ABCにおいて、頂点A,B,Cに向かい合う辺の長さをそれぞれa,b,cとするち、以下の3つの等式が成り立つ。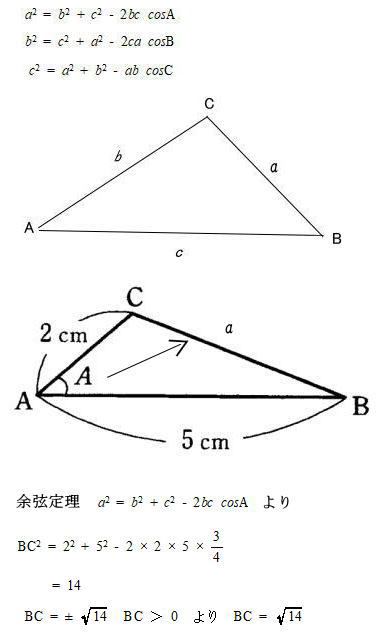
答え エ 1 オ 4
高等学校卒業程度認定試験令和3年度数学問題5.三角関数(5)解説解答
(5) 半径2cmの円Oに内接する正五角形の面積はおよそ[カ]c㎡である。次の①~④のうちから最も適切なものを一つ選べ。必要であれば、次の三角比の値を利用すること。
sin72° = 0.9511 cos72° = 0.3090 tan72° = 3.0777
① 3.1 ② 9.5 ③ 12.6 ④ 30.8
解説解答
sinを用いた三角形の面積公式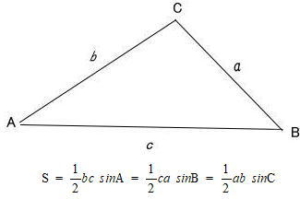
sinを用いた三角形の面積公式より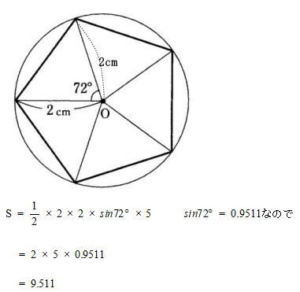
答え ②
