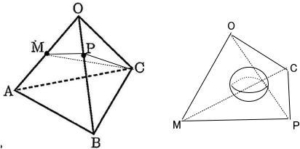
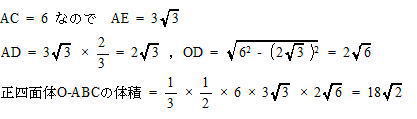2022年度明治大学付属明治高等学校一般入試は志願者男子311名 女子270名 受験者男子290名 女子262名 合格者男子162名 女子111名でした。
一般入試成績は
国語配点100点 受験者平均点45.10点 合格者平均点49.13点 合格者最低点30点
数学配点100点 受験者平均点32.32点 合格者平均点43.81点 合格者最低点10点
英語配点100点 受験者平均点75.20点 合格者平均点86.55点 合格者最低点56点 でした。
2022年度数学入試問題は 1.小問集合5問 2.2次方程式 3.平面図形(円の性質) 4.関数 5.立体図形
例年通り5題構成で,出題内容も大幅な変更はありませんでした。
今回は 明治大学付属明治高等学校数学頻出の 5.立体図形(正四面体)を解説します。
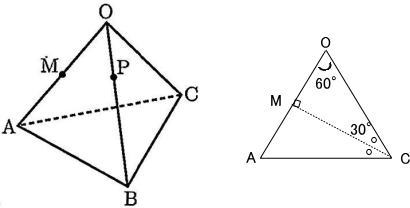
明治大学付属明治高校2022年度数学入試問題5.正四面体 問題
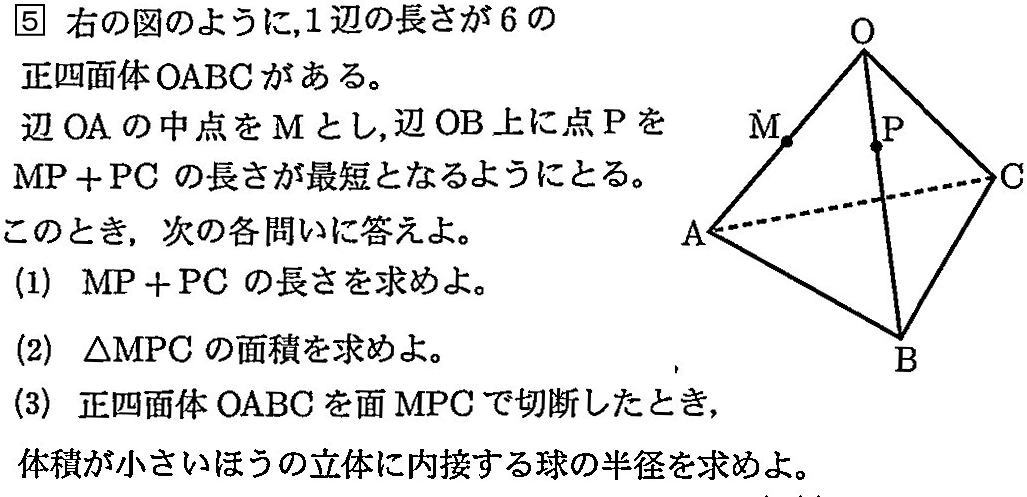
明治大学付属明治高校2022年度数学入試問題5.正四面体 (1)解説解答
(1) MP + PCの長さを求めよ。
解説解答
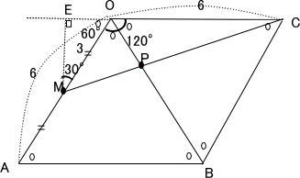
辺OCの延長線に点Mから垂線を下ろしその交点をEとする。
△OEMは ∠MOC = 60°,∠OEM = 90°,∠EMO = 30°の直角三角形
OM = 3 なので 辺の比より
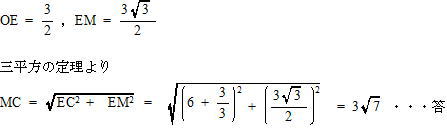
解説解答

辺OCの延長線に点Mから垂線を下ろしその交点をEとする。
△OEMは ∠MOC = 60°,∠OEM = 90°,∠EMO = 30°の直角三角形
OM = 3 なので 辺の比より
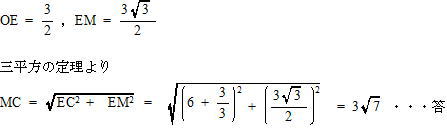
明治大学付属明治高校2022年度数学入試問題5.正四面体 (2)解説解答
(2) △MPCの面積を求めよ。
解説解答
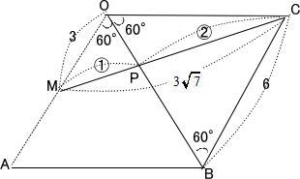
△MOPと△OBPにおいて
∠MOP = ∠CBP = 60°,∠OPM = ∠BPC (対頂角) 二角相等なので △MOP ∽ △OBP
よって 辺の比は MO:BC = MP:CP = 3:6 = 1:2
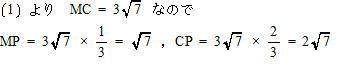
また △OACは正三角形であり、Mは中点なので 二等辺三角形の性質より
∠OCM = ∠ACM = 30°,∠CMO = 90°,∠MOC = 60° よって △OMCは各辺の比より
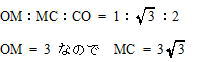
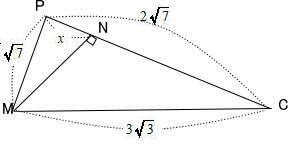
△MPCにおいて、MからPCに垂線を下ろしその交点をNとする。
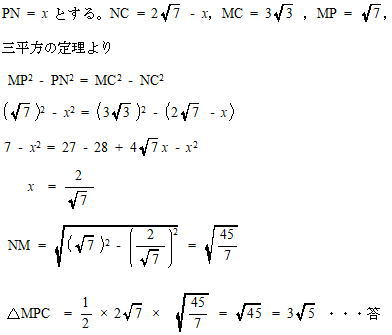
明治大学付属明治高校2022年度数学入試問題5.正四面体 (3)解説解答
解説解答
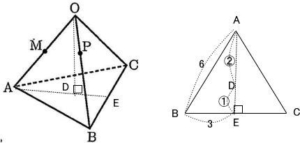
頂点Oから△ABCに垂線を下ろし、その交点をD,辺BCの中点をEとする。
点Dは正三角形ABCの重点になっているので、AD:DE = 2:1