國學院中学入試問題傾向と対策

2022年9月6日、国学院久我山中学高等学校は杏林大学（三鷹市）と「高大連携協定」を締結しました。大学の公開講座への聴講生の受け入れ、大学教員による出張授業、教育についての情報交換や交流など、様々な活動を継続的に行うことが可能になります。「探究学習」をはじめ、生徒の皆さんにとって有意義な学びの機会を提供し、新たな時代にふさわしい高大連携を推進していきます。
　杏林大学は、本校の近隣に位置し、「医」の道を志す学生の学び舎として1966年に開設しました。医学部、保健学部、総合政策学部、外国語学部４学部を擁し、「医学部付属病院」は日本有数の規模を誇る「高度救命救急センター」を備え、東京西部地区の中核病院として地域を支えています。

2022年度第１回入学試験は　募集人数男子一般45名　女子CC 25名に対し　応募者数　男子一般191名　女子CC 97名　受験者　男子一般183名　女子CC 89名　合格者男子一般50名　女子CC42名でした。

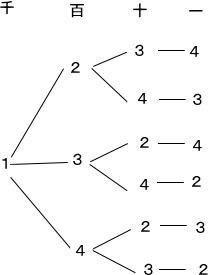
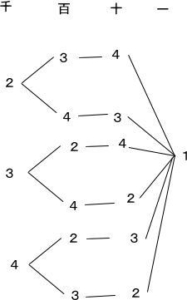
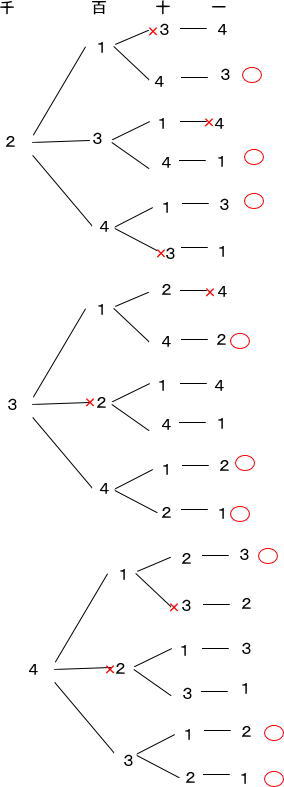
2022年度第１回算数入試問題は大問4題構成で、1.四則計算4問　2.小問集合7問　3.場合の数　4.水そう算が出題されました。
算数の受験者平均点男子一般71.7点　女子CC65.8点　合格者平均点男子一般85.6点　女子CC 73.8点でした。

プロ家庭教師集団スペースONEの中学受験合格のための過去問傾向と対策へ

今回は　3.場合の数を解説します。

[3]　1．2，3，4のカードが1枚ずつあり、この4枚のカードを並べて4けたの整数をつくります。次の問いに答えなさい。

(1)　できる整数は全部で何個ですか。

(2)　できる整数のうち、奇数は全部で何個ですか。

(3)　次のルールにしたがって、4けたの整数をつくります。

ルール　
　・千の位には1のカードを置かない。
　・百の位には2のカードを置かない。　
　・十の位には3のカードを置かない。
　・一の位には4のカードを置かない。

①　このとき、できる整数は全部で何個ですか。

②　①で、できる整数をすべて加えいるといくつになりますか。