女子美術大学付属中学校算数過去問研究

2023年度女子美術大学付属中学生徒募集に関し、5月31日家庭教師学習塾向け入試説明会が実施されました。

来年度から美術教育を期間とした脂質・能力の億世と英語教育をより一層充実させるため、中学では１．新カリキュラムの導入として　英語の授業を3年間で2時間増加。英語教育で一部の授業で少人数の授業を展開。ICT教育の充実として　電子黒板の設置と１人１台タブレットを購入し授業を展開する　以上新しい取り組みについて説明がありました。

2022年度女子美術大学付属中学校第1回入試は　募集人数110名に対し、

2科応募者178名　受験者176名　合格者52名　補欠14名　入学者52名　繰り上げ合格者5名
4科応募者178名　受験者175名　合格者69名　補欠12名　入学者69名　繰り上げ合格者4名

第2回入試は　募集人数10名程度に対し、応募者224名　受験者143名　合格者10名　補欠5名　入学者10名　繰り上げ合格者0名

第3回入試は　募集人数15名程度に対し、応募者347名　受験者187名　合格者13名　補欠7名　入学者13名　繰り上げ合格者1名


第3回入学試験は2科目受験で、第3回科目別合格者平均点は　国語80.1点　算数80.9点、合格者平均点158.6点　受験者平均点118.4点でした。

女子美術大学付属中学の出題傾向に大幅穴変更はありません。過去問を研究し不得意な分野は類題を解いて苦手分野をなくしましょう。

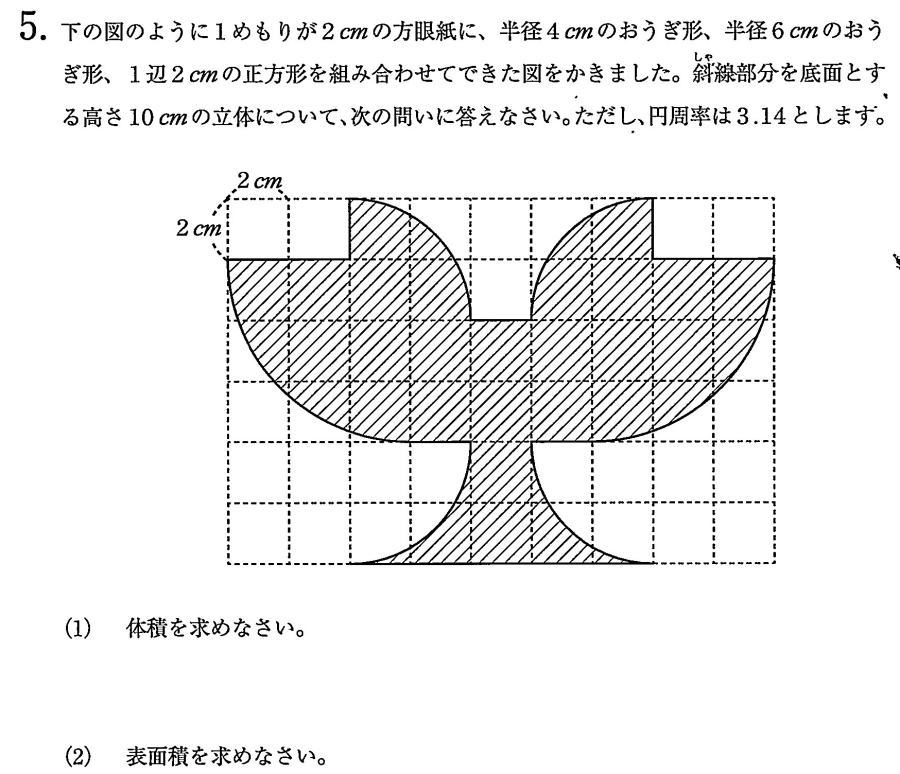
2022年度第3回算数入試問題は　1.小問集合10問 2.規則性　3.割合の文章題　4. 速さのグラフ平面上の点移動5.図形問題(底面積から体積と表面積を求める問題)が出題されました。

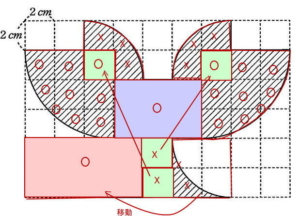
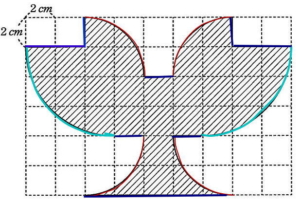
今回は　算数入試問題から5.図形問題(底面積から体積と表面積を求める問題)を解説します。面積を移動して底面積を求めやすくしましょう。