桜蔭中学過去問傾向と対策
令和4年度桜蔭中学校入学試験は2月1日に実施されました。
令和4年度出願者は557名(前年比-24名),受験者534名(前年比-27名),合格者282名(前年比-1名),補欠29名(前年比-4名)でした。
令和4年度算数入試問題は例年通り 大問4題構成で、Ⅰ四則計算を含む小問集合,1.還元算,2.回転図形,3.規則性(フィボナッチ数列) Ⅱ 時計算,Ⅲ 流水算, Ⅳ 立体図形が出題されました。
出題傾向に変化がありませんので、桜蔭中学を志望する受験生は過去問対策をとりましょう。
今回は Ⅲ 流水算を解説します。(1)(2)は非常に平易な問題です。
桜蔭中学校2022年度算数入試問題Ⅲ流水算 問題
桜蔭中学校2022年度算数入試問題Ⅲ流水算 (1)解説解答
(1) 静水時の船の速さは分速何mですか。。
解説解答
静水時のの船の速さ:川の流れの速さ = 4:1
よって 静水時のの船の速さ:船の上りの速さ:船の下りの速さ:川の流れの速さ = 4:4 – 1:4 + 1:1 = 4:3:5:1
Pは A→C間を25分で進み、途中5分間休むので、PがA→C間を下るのにかかる時間は 25 – 5 = 20分
5000mを20分間で下るので 下りの速さは 5000÷20 = 250m/分![]()
答 分速 200m
桜蔭中学校2022年度算数入試問題Ⅲ流水算 (2) 解説解答
(2) P,Qは、2地点B,Cの間で初めて出会いました。その地点をDとするとき、AD間の距離は何mですか。
解説解答
(1)より静水時の船の速さが 分速200m、下りの速さは分速250mなので ![]()
PはQと地点B,C間で初めて出会う前に地点Bで5分間休んでいる。仮にPが休まなかった場合、Pは分速250mで5分間長く進むことができるので
下図の通り Pは地点Aより 250×5 = 1250m遠くから出発したと考えると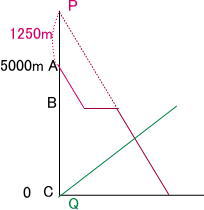
1250 + 5000 = 6250mをPとQが同時に出発して出会ったのと同じになるので、P,Qが出会うのにかかる時間は出発後
桜蔭中学校2022年度算数入試問題Ⅲ流水算 (3) 解説解答
(3) P,Qが2回目に出会ったのは地点Bでした。このとき、PはちょうどBを出発するところで、QはちょうどBに着いたところでした。AB間の距離は何mですか。
解説解答
P,Qが2回目に出会うまでにPは3回,Qは2回休んでいる。このとき、PはちょうどBを出発するところで、QはちょうどBに着いたところだったので、Pが1回,Qが休まないとPとQは同時にB地点で出会うことになる。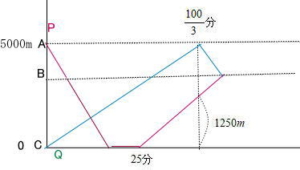
QがCから下ってAにつくのにかかる時間![]()
PがAから下ってCに着くのにかかる時間は
5000÷25 = 20分
Pが1回休んでCから上り始めるのは 20 + 5 = 25分
残り5000 – 1250 = 3750mをPとQは同時に出会い始めるので

