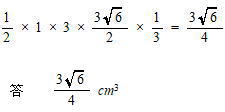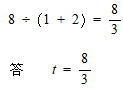慶應義塾高校入試問題研究
慶應義塾高等学校2021年度数学入試問題は昨年同様大問7題構成で、1.小問集合,2.平面図形3問,3.展開図と立体図形,4.場合の数,5.塩酸記号,6.関数,7.四面体と点移動が出題されました。全範囲から満遍なく出題されていますので、教科書の全範囲を復習しましょう。
今回は7四面体と点移動を解説します。
慶応義塾高校2021年度数学入試問題7.四面体と点移動 問題
慶応義塾高校2021年度数学入試問題7.四面体と点移動 (1)解説解答
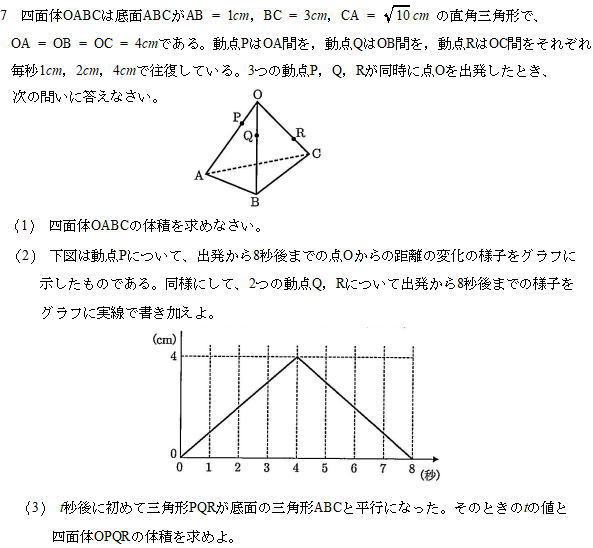
(1) 四面体OABCの体積を求めなさい。
解説解答
頂点から直角三角形ABCに垂線をおろしその交点をHとする。
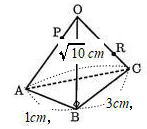
点Hは直角三角形のAC上にあり、AH = HCとなる。
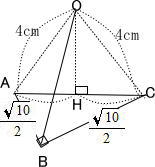
直角三角形OAHにおいて、三平方の定理より
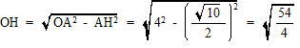
したがって 四面体ABCの体積は
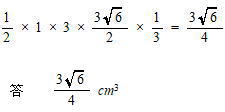
慶応義塾高校2021年度数学入試問題7.四面体と点移動 問題(2)解説解答
解説解答
動点Qの速さは 秒速2cm,OB = 4cmなので、O→Bを2秒,B→Oを2秒で往復する。
動点Rは 秒速4cm,OC = 4cmなので、O→Cを1秒,C→Oを1秒で往復する。
答
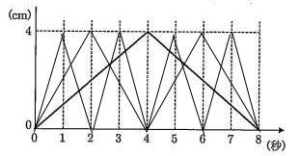
慶応義塾高校2021年度数学入試問題7.四面体と点移動 (3)解説解答
(3) t秒後に初めて三角形PQRが底面の三角形ABCと平行になった。そのときのtの値と四面体OPQRの体積を求めよ。
t 解説解答
三角形PQRが底面の三角形ABCと平行になるのは、OP = OQ = ORとなるとき。よって下図の通り〇のとき。初めて平行になるのは 2 < t < 3のとき。。
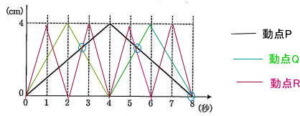
下図の様に、相似比より
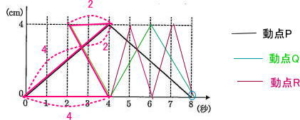

別解
動点Pと動点Rは初めてOP = PRとなるとき、動点Pと動点Rは合わせて8cm動いている。
よって
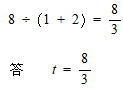
四面体OPQRの体積 解説解答