桐光学園中学校帰国生入試過去問研究
桐光学園中学校帰国生入試の受験資格は下の条件をすべて満たしていることです。①保護者の海外在留に伴う海外在住期間が通年1年以上で,2018年1⽉以降に帰国した者。またはそれに準ずる者。もしくは,国内インターナショナルスクールに4年以上在籍している者。
②入学後,保護者もしくはそれに準ずるところから通学可能な者。
試験科目は
①国語・算数・英語から選択した2科目 8:50〜10:10 (80分/各100点)
②受験生面接 10:40〜です。
2021年度帰国生入学試験応募者 男子87名 女子22名 受験者数男子85名 女子21名 合格者男子52名(内特待生7名) 女子12名(内特待生1名)でした。
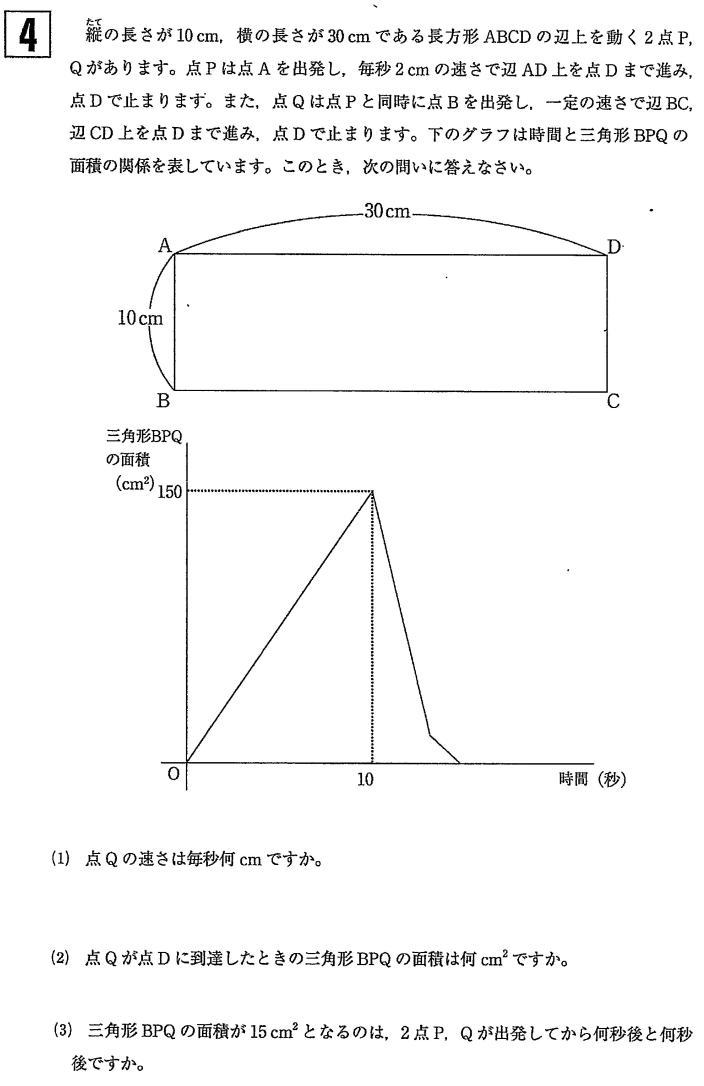
2021年度 桐光学園中学校帰国生算数入試問題は 例年通り大問4題構成。1.小問集合7問 2.倍数の文章題 3.約束記号(約数) 4.平面上の点移動 が出題されました。
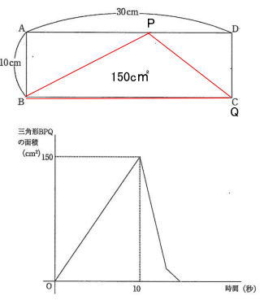
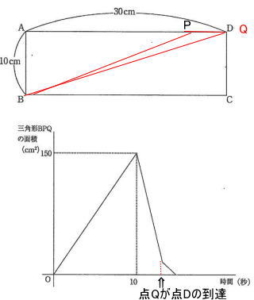
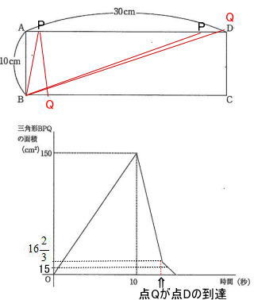
今回は 4.平面上の点移動を解説します。 グラフの読み取りが重要です。