成蹊高等学校過去問研究
2021年度成蹊高等学校一般入学試験は、応募者男子109名,女子86名,受験者男子106名,女子86名,合格者男子48名,合格者47名でした。
数学一般入試は最高点95点,受験者平均点68.6点,合格者平均点80.6点でした。
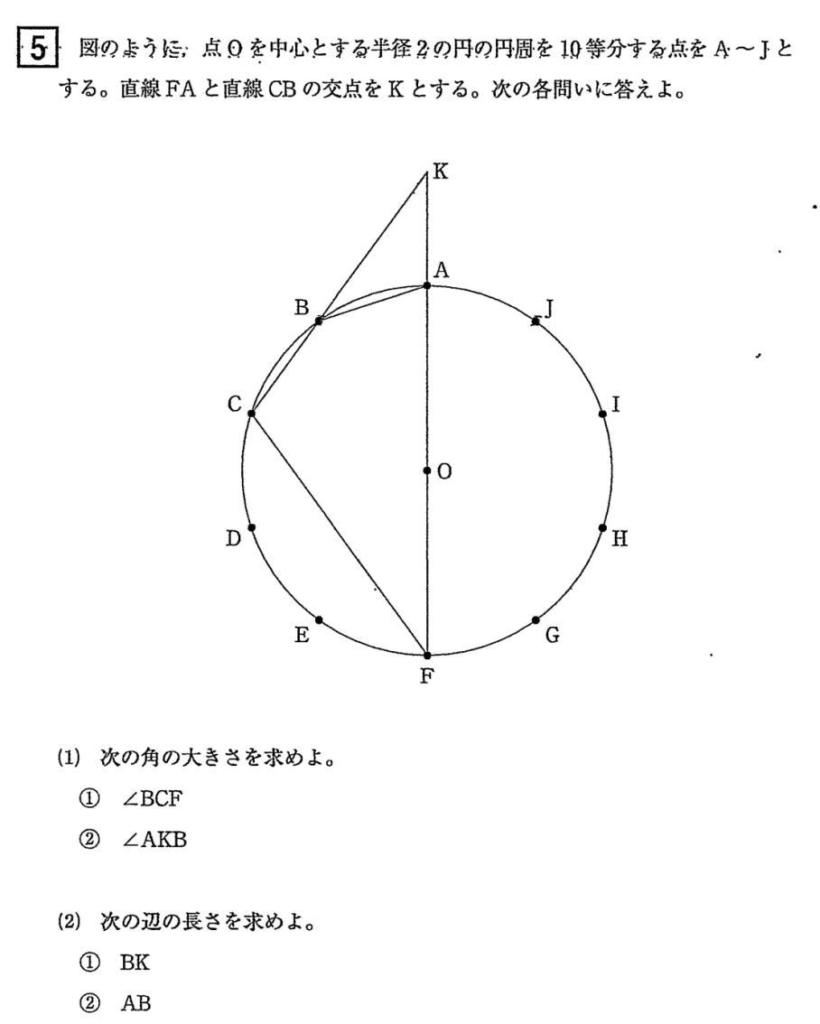
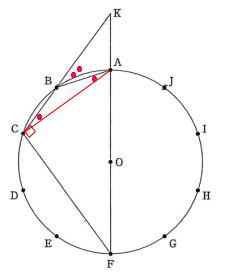
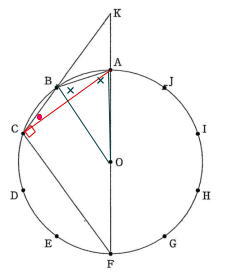
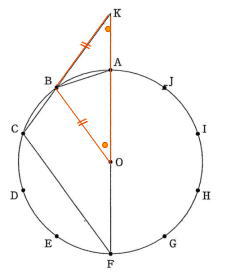
問題は例年同様大問5題構成で、出題内容も昨年通り1.小問集合5問 2.方程式の応用 3.確率 4.関数のグラフ 5.平面図形(円の性質) でした。
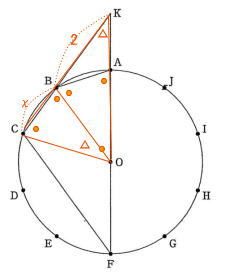
今回は5.平面図形を解説します。円を等分したときの円周角の大きさなどの基礎事項はしっかり確認して使いこなせるようにしましょう。