東京都立青山高等学校独自作成問題傾向と対策
2020年度をもってグループ作成問題は廃止されますが、 進学指導特別推進校(日比谷高校・西高校・国立高校・八王子東高校・戸山高校・青山高校・立川高校)と進学指導特別推進校(新宿高校・進学重視型単位制高校の国分寺高校)、進学指導推進校(進学重視型単位制高校の墨田川高校)が国語・数学・英語3科目とも自校作成問題となります。
都立青山高校受験生は独自作成問題を通して合格対策をとりましょう。
2021年度都立青山高校数学入試問題は、例年通りの出題構成で、内容は1.小問集合5問 2.関数とグラフ 3.平面図形(円の性質) 4.空間図形(四角すいの体積の誘導問題)でした。
今回は 2.関数のグラフを解説します。
都立青山高校2021年度独自作成数学考査問題2.関数のグラフ 問題
都立青山高校2021年度独自作成数学考査問題2.関数のグラフ 問1.解説解答
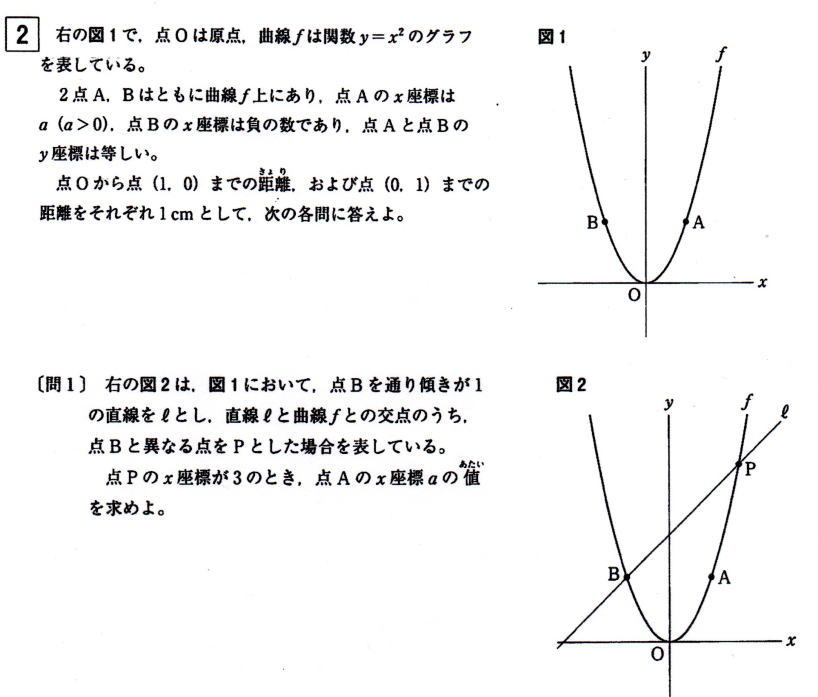
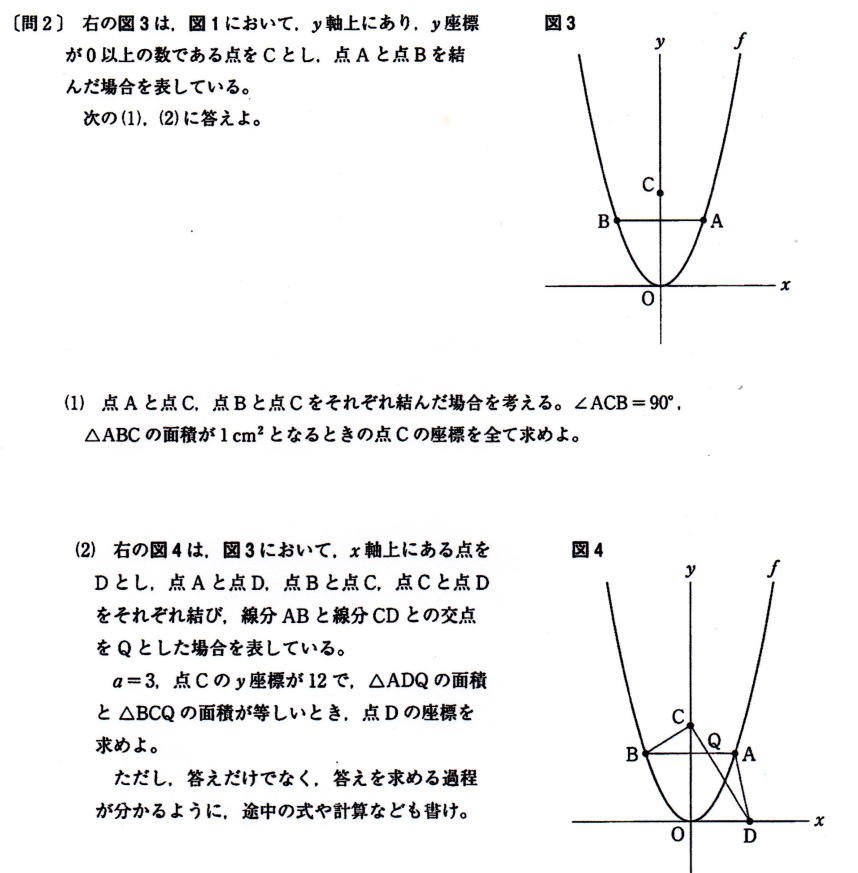
[問1] 図2は図1において、点Bを通り傾きが1の直線ℓとし、直線ℓと曲線fとの交点のうち、点Bと異なる点をPとした場合を表している。点Pのx座標が3のとき、点Aのx座標aの値を求めよ。
解説解答
解説解答
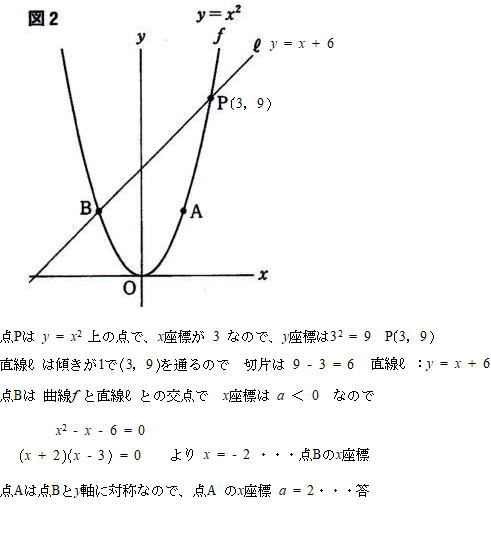
都立青山高校2021年度独自作成数学考査問題2.関数のグラフ 問2.(1)解説解答
解説解答
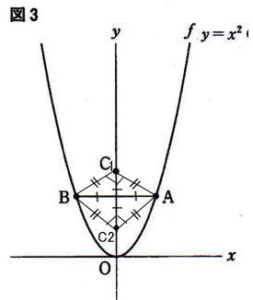
∠ACB = 90°となるとき△ABCは直角二等辺三角形となる。図のようにy軸上に条件を満たす点C1,C2をおく。点C1と点C2は直線ABに対称でy軸上の点。
△ABC1,△ABC2は直角二等辺三角形なので、四角形AC1BC2は正方形。
正方形の面積 = 対角線×対角線÷2 なので 正方形AC1BC2の面積は2
よって 対角線AB×対角線C1C2 =4 したがって AB = C1C2 = 2
直線AB = 2となるとき 点Aのx座標は 1,点Bのx座標は – 1,よって点A,Bのy座標は1
したがって 点C1のy座標は 1 + 1 = 2,点C2のy座標は 1- 1 = 0
答 (0,0) (0,2)
都立青山高校2021年度独自作成数学考査問題2.関数のグラフ 問2(2)解説解答
問2 (2) 右の図4は、図3において、x軸上にある点をDとし、点Aと点D,点Bと点C,点Cと点Dをそれぞれ結び、線分1ABと線分CDとの交点をQとした場合を表している。
a = 3,点Cのy座標が12で、△ADQの面積と△BCQの面積が等しいとき、点Dの座標を求めよ。
解説解答
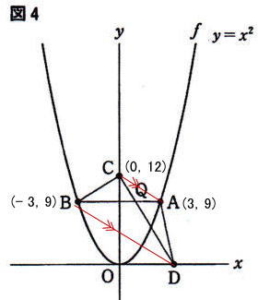
△ADBと△BCDにおいて
△ADB = △ADQ + △QDB,△BCD = △BCQ + △QDB
△ADQの面積 = △BCQの面積(仮定),△QDB(共通) なので △ADBの面積 = △BCDの面積
よって 直線BDの傾き = 直線CAの傾き
a = 3 なので A(3,9),B(- 3,9) 仮定よりC(0,12)なので
直線BCは点B(- 3,9)を通るので、切片は 9 – ( – 1)×( – 3) = 6
よって 直線BDの式は y = – x + 6
点Dは直線 y = – x + 6 とx軸との交点なので - x + 6 = 0 よって x = 6
答 (6,0)
