芝中学校過去問傾向と対策

2021年度第１回入学試験は募集人数150名に対し、応募者491名，受験者445名，合格者187名

第１回算数受験者最高点95点，受験者平均点53.3点，合格者平均点68.6点でした。

算数入試問題は1.四則計算2問，2.食塩の濃度，3.数の性質，4.損益売買，5.平面図形，6.約束記号，7.場合の数，8.ニュートン算が出題されました。

今回は　8.ニュートン算を解説します。

芝中学校2021年度算数入試問題8.ニュートン算　問題

８．あるホールでコンサートが行われました。受け付けは開演の1時間前から行われ、受け付け開始前にすでに480人が並んでいました。受付開始後も一定の割合で人を入場させます。受付を開始したときは、受付場所を5カ所開け、その10分後には並んでいる人は300人になりました。受付開始20分後に5カ所の受付場所を4カ所にしたところ、開園の20分前には並んでいる人がいなくなりました。

(1)　受付開始20分後には□人が並んでいました。

(2)　1分間に□人が列に加わります。

芝中学校2021年度算数入試問題8.ニュートン算 (1)　解説解答

(1)　受付開始20分後には□人が並んでいました。

解説解答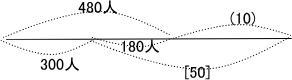



1分間に列に並ぶ人数を(1)とすると、10分間に列に加わる人数は　(1)×10 = (10)

1つの受付場所が1分間に受け付ける人数を[1]とすると、5つの窓口で10分間に受け付ける人数は　[1]×5×10 = [50]

よって　5つの窓口で10分間に受け付ける人数は

[50] = 480 – 300 + (10) = 180 + (10)

したがって　20分間に5つの受付場所で受け付ける人数は　[1]×5×20 = [100] = [50]×2 なので

(180 + (10))×2 = 180×2 + (10)×2 = 360 + (20)

よって　並んでいる人数は　480 – 360 = 120

答　　120人

芝中学校2021年度算数入試問題8.ニュートン算　(2)　解説解答

(2)　1分間に□人が列に加わります。

解説解答

開演60分前から開演40分前までの20分間に5つの窓口で受け付ける人数は 480 – 120 = 360人と列に加わる人数(20)

開演40分前から開演20分前までの20分間に4つの窓口で受け付ける人数は 120人と列に加わる人数(20)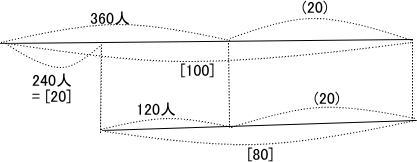




線分図より　[100] – [80] = 360 – 120
　　　　　　　　　　[20] = 240　　よって　窓口1つが1分間に受け付ける人数は[1] = 240÷20 = 12人

[80] = 120 + (20)
12×80 = 120 + (20)

(20) = 960 – 120 = 840　　よって　1分ごとに列に加わる人数は　840÷20 = 41人


答　　　41人