2021年度都立新宿高等学校は、推薦入試募集人数男女32名に対し、応募者男子41名,女子106名,合格者数男子8名,女子24名でした。
学力権者による入学者は、募集人数男女284名に対し、受験者数男子240名 女子247名,合格者数男子142名,女子146名でした。
独自数学入試問題は1.小問集合6問,2.関数のグラフ 3.平面図形(証明問題を含む) 4.場合の数と確率でした。
今回は4 場合の数と確率を解説します。数え上げは表を使う場合も解説します。
都立新宿高校2021年度 数学入試問題 4.座標平面と確率 問題
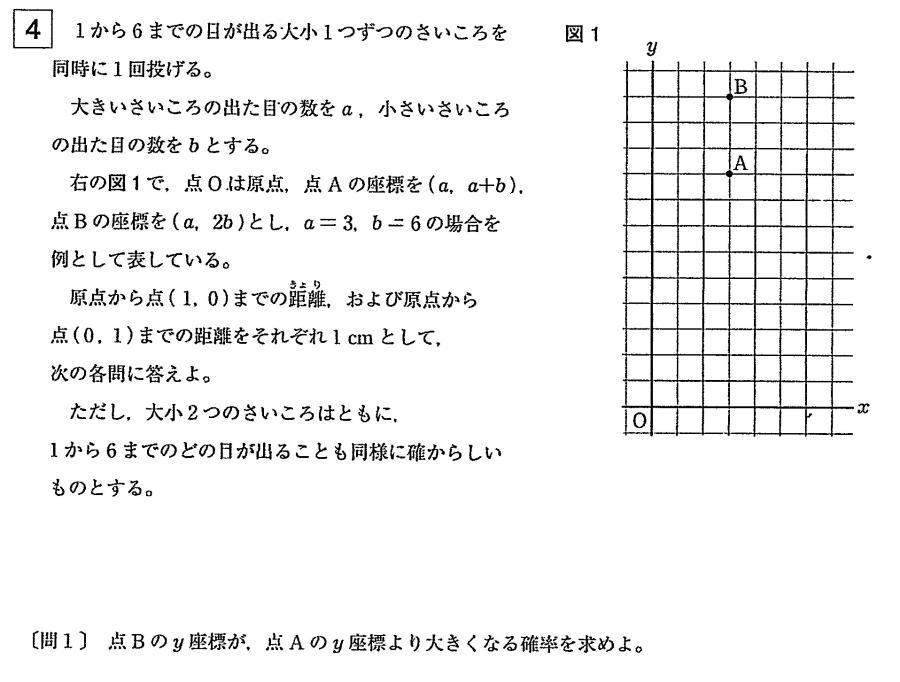
都立新宿高校2021年度 数学入試問題 4.場合の数と確率 問1解説解答
解説
a + b < 2b なので
a = 1のとき b = 2,3,4,5,6
a = 2のとき b = 3,4,5,6
a = 3のとき b = 4,5,6
a = 4のとき b = 5,6
a = 5のとき b = 6
a = 1のとき b なし
以上 15通り
または 下の表の通り
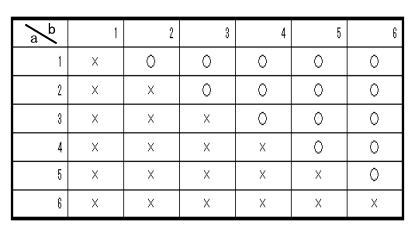
したがって 確率は
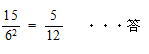
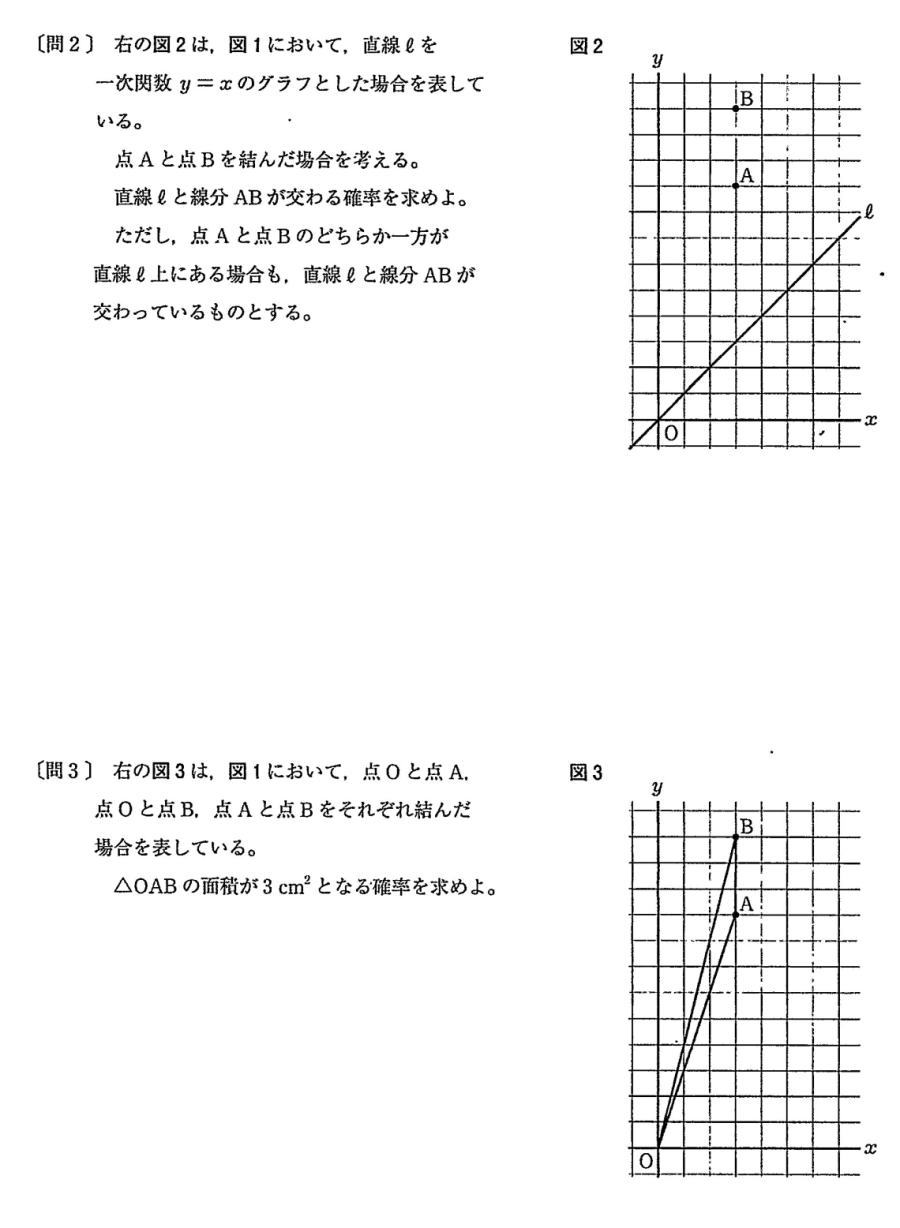
都立新宿高校2021年度 数学入試問題 4.場合の数と確率 問2 解説解答
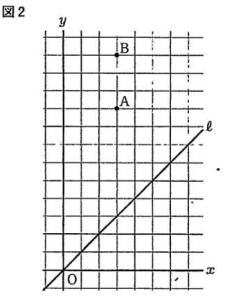
解説解答
点Aの座標(a,a + b) 点Bの座標(a,2b) なので、点ABともにx座標は a,
よって直線ℓと線分ABが交わる場合は
ⅰ) a + b ≦ a ≦ 2 b
点Aのy座標より点Bのy座標が大きく2点間を y = xが通るとき。a≩ 1 なので不能
ⅱ) 2b≦a≦a + b
点Bのy座標より点Aのyざひょうが大きく2点間をy = xが通るとき
a≦a + bは常に成立する。よって2b≦aとなる場合
(a,b)とすると、(2,1)(3,1)(4,1)(5,1)(6,1)(4,2)(5,2)(6,2) 以上9通り
または 下の表の通り
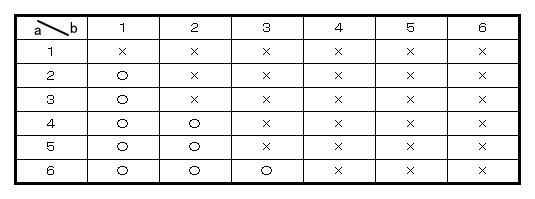
したがって 確率は
都立新宿高校2021年度 数学入試問題 4.場合の数と確率 問3解説解答
問3 右の図3は、図1において、点Oと点A,点Oと点B,点Aと点Bをそれぞれ結んだ場合を表している。△OABの面積が3c㎡となる確率を求めよ。
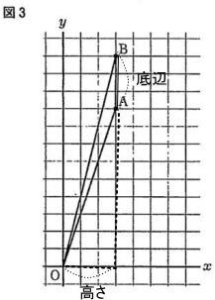
解説解答
点Aの座標(a,a + b) 点Bの座標(a,2b) なので、高さを原点Oと点ABのx座標の差 aとした場合,底辺は点Aと点Bのy座標の差となる。
よって
ⅰ) 点Aのy座標より点Bのy座標が大きい場合
a + b>2b よって底辺の長さは a + b – 2b = a – b
したがって △OABの面積が3c㎡となるのは b < a かつ a(a-b) = 6
ⅱ) 点Bのy座標より点Aのyざひょうが大きい場合
a + b <2b よって底辺の長さは 2b – (a + b) = b – a
したがって △OABの面積が3c㎡となるのは a < b かつ a(b – a) = 6
以上より (a,b)とすると、(2,5)(3,5)(5,2)(5,3) 以上4通り
よって 確率は
