MENU

記事の作成者：プロ家庭教師集団スペースONEとは

最新情報

  • HOME
    •  > 
  • 過去問対策
    •  > 
  • 芝浦工大附属高校2021年度数学入試問題3.立体上の点移動

    • 2021/06/14

    • 高
    • オ
    • 過去問対策

    芝浦工大附属高校2021年度数学入試問題3.立体上の点移動

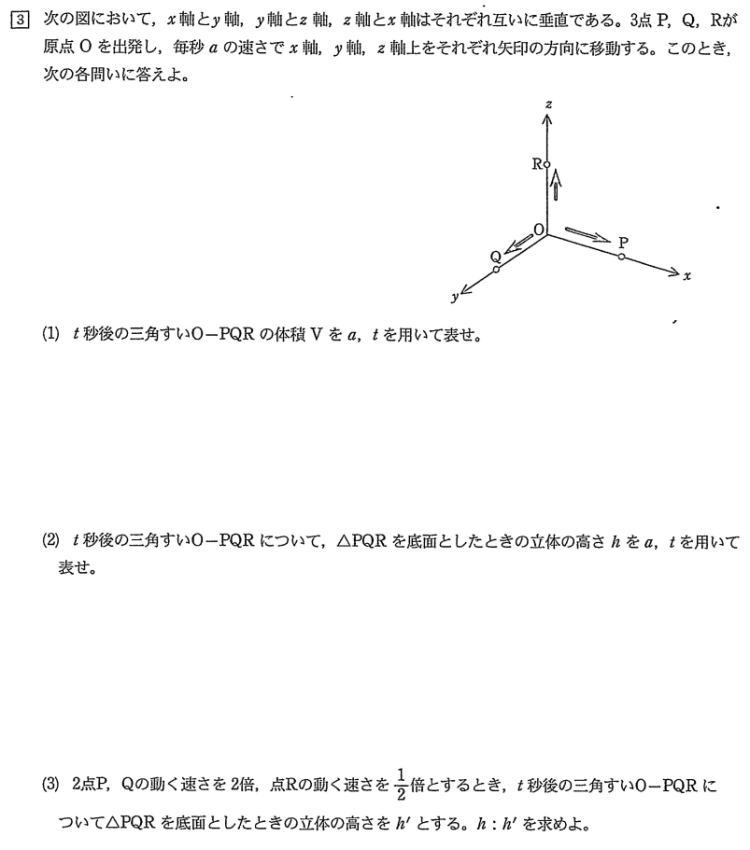
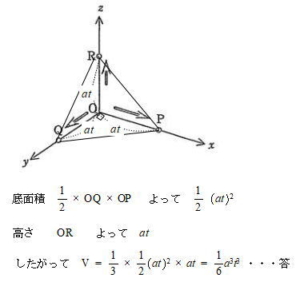
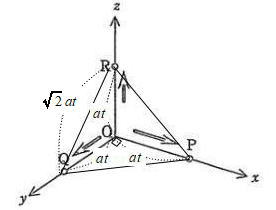
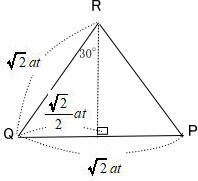
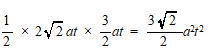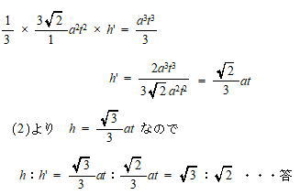    芝浦工業大学附属高校過去問研究

     

    プロ家庭教師集団スペースONEの高校入試問題解説解答へ

     

    芝浦工業大学附属高校一般入学試験数学は、基礎数学30分(100点満点)，応用数学50分(100点満点)が課せられます。

    2021年度は数学基礎受験者受験者最高点100点，受験者最低点7点，受験者平均点68.7点，合格者平均点87.0点，合格者平均点87.9点

    応用数学は受験者最高点82点，受験者最低点3点，受験者平均点41.5点，合格者平均点61.7点でした。

    出題内容は　基礎数学小問13問，応用数学は1.関数の変域と変化の割合，2.平面図形(含証明問題)，3.立体上の点移動，4.平面図形(円の性質)の大問4題構成でした。

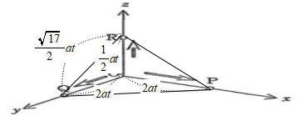
    今回は応用数学3.立体上の点移動を解説します。

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

    芝浦工業大学附属高校2021年度応用数学入試問題3.立体上の点移動　問題

    芝浦工業大学附属高校2021年度応用数学入試問題3.立体上の点移動　(1)　解説解答

     
    (1)　t秒後の三角すいO-PQRの体積Vをa，tを用いて表せ。

    解説解答

    t秒後のOQ = OP = ORの長さは　at






    芝浦工業大学附属高校2021年度応用数学入試問題3.立体上の点移動(2)　解説解答


    (2)　t秒後の三角すいO-PQRについて、△PQRを底面としたときの立体の高さhをa，tを用いて表せ。

    解説解答



    OR = OQ，∠QOR = 90°なので△ORQは直角二等辺三角形　よって　辺の比より



    △ORQ ≡ △OQR ≡ = △OPRなので、△PQRは正三角形



    よって図の通りQPを底辺とするとき高さは



    よって　△RQPの面積は




    △PQRを底辺としたときの高さhは

    芝浦工業大学附属高校2021年度応用数学入試問題3.立体上の点移動(3)　解説解答


    (3)　2点P，Qの動く速さを2倍，点Rの動く速さを1/2倍とするとき、t秒後の三角すい-PQRについて△PQRを底面としたときの立体の高さをh’とする。h：h’を求めよ。

    解説解答




    t秒後のOQ，OP，ORの長さは





    また△RQPにおいて、三平方の定理より



    また　△OQPは、OQ = OP，∠QOP = 90°の直角二等辺三角形なので、辺の比より



    QPを底辺としたときの高さは　三平方の定理より






    よって　△RQPの面積は


    よって△RQPを底面積としたときの高さ h’は

    合格者お喜びの声はこちら

    各種お問い合わせにつきましては、下記よりお気楽にお問い合わせください。

    お問い合わせはこちら
    メールでお問い合わせ
    LINEでお問い合わせ

    オンライン家庭教師も在籍中！「お問い合わせ種別」の欄を選択ください。

    営業時間：AM 10:00 〜PM 9:00