慶応義塾湘南藤沢高等部帰国枠過去問傾向と対策
帰国枠では選考方法は、出願書類、筆記試験(国語「課題型小論文」45 分、 数学 45 分)、および面接になります。
数学は、過去問で出題傾向を確認し本番に備えましょう。
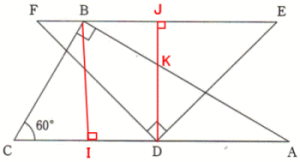
慶応湘南藤沢高等部2020年度帰国生数学入試問題5.平面図形 問題
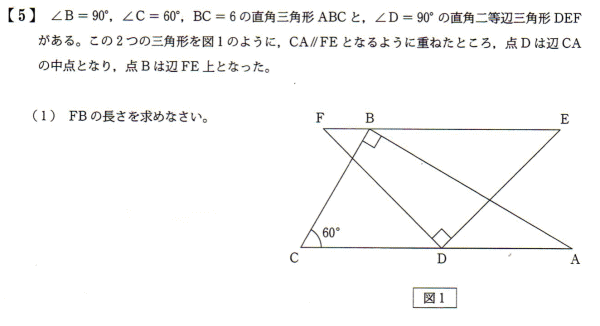
慶応湘南藤沢高等部2020年度数学入試問題5.平面図形 解説解答 1.相似比を用いた解答
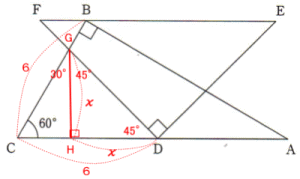
△BCAは∠B = 90°,∠C = 60°より∠A = 30°の直角三角形なので、辺の比よりCA = 12,
点Dは辺CAの中点なので、CD = 6
△DEFは直角二等辺三角形なので ∠F = 45°
よって∠F = ∠FDC = 45°(平行線の錯角)
辺BCと辺FDの交点をGとし、点GからCDに垂線を下しその交点をHとする。
△GHDは∠GHD = 60°,∠CHG = 90°より∠HGC = 30°なので
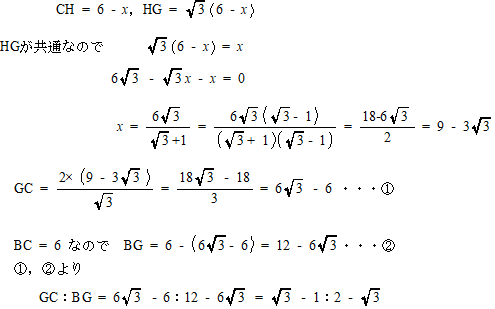
△FBG∽△DCGなので FB:BG = DC:CG
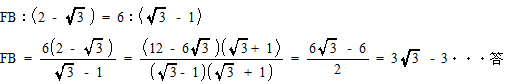
慶応湘南藤沢高等部2020年度数学入試問題5.平面図形 別解
DJとABとの交点をKとする。

プロ家庭教師集団スペースONEの高校入試問題解説解答へ
