MENU

記事の作成者：プロ家庭教師集団スペースONEとは

最新情報

  • HOME
    •  > 
  • 過去問対策
    •  > 
  • 女子美術大学付属中学校2021年度算数入試問題1.小問集合(8)～(10)平面図形3問

    • 2021/06/05

    • 中
    • オ
    • 過去問対策

    女子美術大学付属中学校2021年度算数入試問題1.小問集合(8)～(10)平面図形3問

    女子美術大学付属中学校算数過去問研究

    2021年度女子美術大学付属中学校第１回入学試験は2月1日に実施されました。

    第3回入学試験は2科目受験で、募集人数約15名に対し志願者数341名　受験者数 189名　合格者数14名でした。

    第3回科目別合格者平均点は　国語80.1点　算数80.9点でした。

    第3回算数入試問題は　1.小問集合10問 2.規則性　3.つるかめ算　4. 速さのグラフ(水そうに水を入れるグラフ)　5. 空間図形の展開図が出題されました。

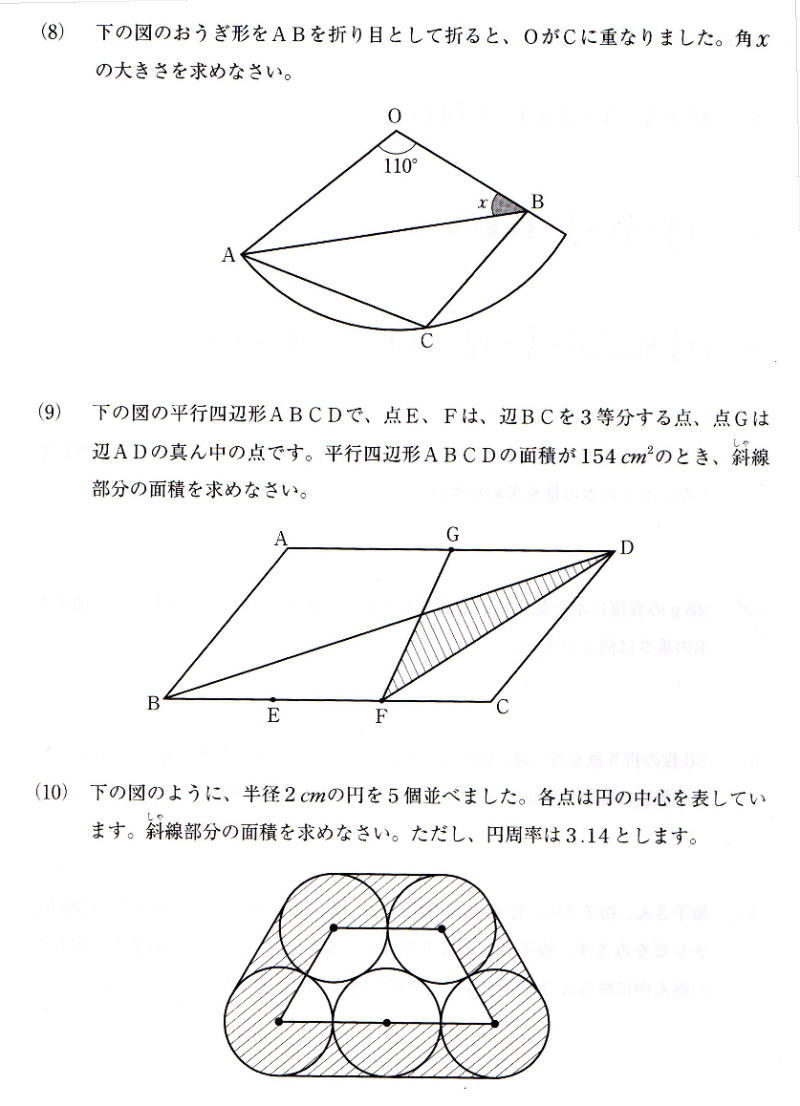
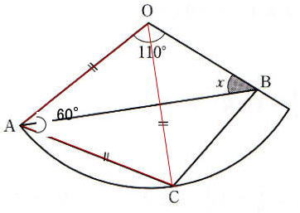
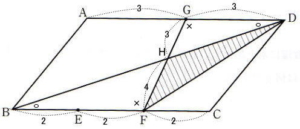
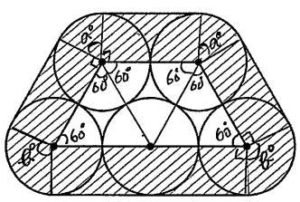
    今回は　算数入試問題から1.小問集合を解説します。小問集合10問で配点は各5点　計50点です。全問正解を目指しましょう。(8)の図形問題はひらめきを要求される出題でしたが、他は中学受験問題集の基本から標準問題を繰り返し解いて練習しておけば必ず解いたことがある問題です。繰り返し算数問題集や過去問を練習して合格を勝ち取ってください。

     

    女子美術大学附属中学校2021年度　算数入試問題1.小問集合(8)～(10)　平面図形3問　問題

    　

    女子美術大学附属中学校2021年度　算数入試問題1.小問集合(8)平面図形の求角　解説解答

    (8)　下の図のおうぎ形をABを折り目として折ると、OがCに重なりました。角xの大きさを求めなさい。

    解説解答

    下図の通り点Oと点Cを直線で結ぶ。



    三角形OACは　OA =OC (おうぎ形の半径) 　また、おうぎ形をABを折り目として折っているので　OA = AC

    よって　三角形OACは、OA = AC = OCなので、正三角形。

    また　角BOA = 角ACB = 110°

    四角形OACBの内角の和は　360°なので、角CBO = 360 – (110×2 + 60) = 80°

    角BOA = 角ACB　なので、角x = 80÷2 = 40°


    答　　　40°

    女子美術大学附属中学校2021年度算数入試問題2.小問集合(9)平面図形の求積　解説解答

    (9)　下の図の平行四辺形ABCDで、点E、Fは、辺BCを3等分する点、点Gは辺ADの真ん中の点です。平行四辺形ABCDの面積が154c㎡のとき、斜線部分の面積を求めなさい。

    解説解答



    点E、Fは、辺BCを3等分する点、点Gは辺ADの真ん中の点であり、平行四辺形の性質よりAD = BCなので　AD = BCの長さを3と2の最小公倍数の6とすると、

    AG：GD：BE：EF：FC = 6÷2：6÷2：6÷3：6÷3：6÷3 = 3：3：2：2：2

    台形ABFGと台形GFCDは高さの等しい四角形なので、底辺の和の比 = 四角形の面積比

    よって　台形ABFGの面積：台形GFCDの面積 = 3 + 2×2：3 + 2 = 7：5・・・①

    三角形DGFと三角形DFCも高さの等しい三角形なので、底辺の比 = 三角形の面積比

    よって　三角形DGFの面積：三角形DFCの面積 = 3：2・・・②

    対角線BDと直線GFの交点をHとすると、三角形DGHと三角形BHFは相似形なので　DG：BF = GH：HF = 3：2×2 = 3：4

    よって　三角形DGHの面積：と三角形DHFの面積 = 3：4・・・③

    ①，②，③より　斜線部分(三角形DHF)の面積は




    答　　22c㎡

    女子美術大学附属中学校2021年度算数入試問題2.小問集合(10)円の性質　解説解答


    (10)　下の図のようも、半径2cmの円を5個並べました。各点は円の中心を表しています。斜線部分の面積を求めなさい。ただし、円周率は3.14とします。

    解説解答



    図の通り円の中心と接点を直線で結び、円の中心と円の中心をそれぞれ結ぶ。

    角a = 360 – (90×2 + 60×2) = 60°

    角b = 360 – (90×2 + 60) = 120°

    よって　斜線部分の面積は横2×2 = 4cm たて2cmの長方形×3と横2×4 = 8cm たて2cmの長方形の面積　+ 中心角60×2 + 120°×2 = 360° 半径2cmの円の面積

    (４×3 + 8)×2 + 2×2×3.14 = 40 + 12.56 = 52.56


    答　　　52.56c㎡
    合格者お喜びの声はこちら

    各種お問い合わせにつきましては、下記よりお気楽にお問い合わせください。

    お問い合わせはこちら
    メールでお問い合わせ
    LINEでお問い合わせ

    オンライン家庭教師も在籍中！「お問い合わせ種別」の欄を選択ください。

    営業時間：AM 10:00 〜PM 9:00