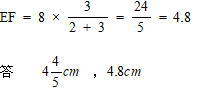日本学園中学校過去問対策

2020年度日本学園中学校2月1日午前入学試験算数入試問題は、例年通りの出題構成で[1] 四則計算6問，[2] 小問集合6問，[3] 立体図形(円柱)，[4] 平面図形，[5] 規則性，[6] 速さのグラフが出題されました。難問奇問はなく、非常にオーソドックスな出題です。中学算数問題の全範囲から満遍なく出題されていますので、算数入試問題集の基本から標準問題を繰り返し勉強し苦手問題がないようにしましょう。

今回は　4.平面図形を解説します。高さの等しい三角形の面積比と底辺の比から解きましょう。

日本学園中学校2020年度算数入試問題4.平面図形　問題

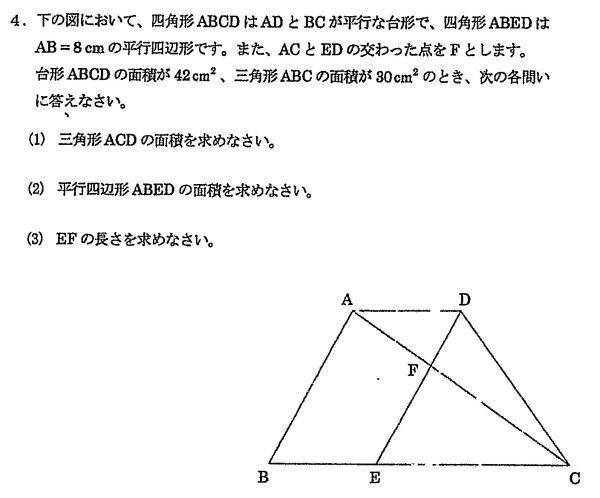
日本学園中学校2020年度算数入試問題4.平面図形 (1) 解説解答

(1) 三角形ACDの面積を求めなさい。

解説解答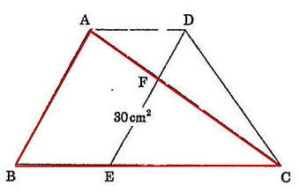



台形ABCD = 三角形ABC + 三角形ACD

台形ABCDの面積 = 42c㎡，三角形ABCの面積 = 30c㎡　なので

三角形ACDの面積 = 42 – 30 = 12


答　　12c㎡

日本学園中学校2020年度算数入試問題4.平面図形　(2)　解説解答　

(2)　平行四辺形ABEDの面積を求めなさい。

解説解答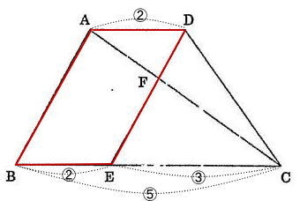



三角形ABCと三角形ACDは高さの等しい三角形なので、面積比 = 底辺の比 = 30：12 = 5：2　

平行四辺形の性質より　AD = BE　なので、AD：Be：BC = 2：2：5 – 2 = 2：2：3

よって　平行四辺形ABEDと三角形DECの面積比は　2 + 2：3 = 4：3

台形ABCDの面積は42c㎡なので、平行四辺形ABEDの面積は



答　　24c㎡

日本学園中学校2020年度算数入試問題4.平面図形　(3)　解説解答

(3)　EFの長さを求めなさい。

解説解答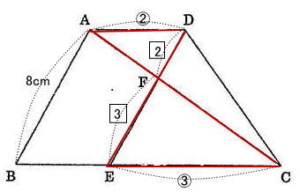



ADとBCは平行なので、三角形AFDと三角形CFEは相似形

AD：CE = 2：3なので　DF：FE = 2：3

平行四辺形の性質より AB = DE = 8cm　なので